
【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入,已知研发投入![]() (十万元)与利润
(十万元)与利润![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系。试求:
呈线性相关关系。试求:
(1)线性回归方程![]() ;
;
(2)估计![]() 时,利润是多少?
时,利润是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式:
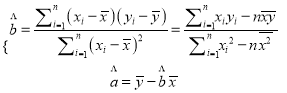
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足: ![]() ,对于
,对于![]() ,都有
,都有![]() (其中
(其中![]() 为常数),则称
为常数),则称![]() 具有性质“
具有性质“![]() ”.
”.
(Ⅰ)若![]() 具有性质“
具有性质“![]() ”,且
”,且![]() ,
, ![]() ,
, ![]() ,求
,求![]() ;
;
(Ⅱ)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() ,判断
,判断![]() 是否具有性质“
是否具有性质“![]() ”,并说明理由;
”,并说明理由;
(Ⅲ)设![]() 既具有性质“
既具有性质“![]() ”,又具有性质“
”,又具有性质“![]() ”,其中
”,其中![]() ,
, ![]() ,
, ![]() 互质,求证:
互质,求证: ![]() 具有性质“
具有性质“![]() ”.
”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“城中观海”是近年来国内很多大中型城市内涝所致的现象,究其原因,除天气因素、城市规划等原因外,城市垃圾杂物也是造成内涝的一个重要原因.暴雨会冲刷城市的垃圾杂物一起进入下水道,据统计,在不考虑其它因素的条件下,某段下水道的排水量V(单位:立方米/小时)是杂物垃圾密度x(单位:千克/立方米)的函数.当下水道的垃圾杂物密度达到2千克/立方米时,会造成堵塞,此时排水量为0;当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时;研究表明,0.2≤x≤2时,排水量V是垃圾杂物密度x的一次函数.
(1)当0≤x≤2时,求函数V(x)的表达式;
(2)当垃圾杂物密度x为多大时,垃圾杂物量(单位时间内通过某段下水道的垃圾杂物量,单位:千克/小时)f(x)=xV(x)可以达到最大,求出这个最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名同学根据各自的样本数据研究变量![]() 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:( )
之间的相关关系,并求得回归直线方程,分别得到以下四个结论:( )
①![]() 与
与![]() 负相关且
负相关且![]() . ②
. ②![]() 与
与![]() 负相关且
负相关且![]()
③![]() 与
与![]() 正相关且
正相关且![]() ④
④![]() 与
与![]() 正相关且
正相关且![]()
其中正确的结论的序号是( )
A. ①② B. ②③ C. ①④ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论中:
(1)如果两个函数都是增函数,那么这两个函数的积运算所得函数为增函数;
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;
(3)既是奇函数又是偶函数的函数只有一个;
(4)若函数f(x)的最小值是a,最大值是b,则f(x)值域为[a,b].
其中正确结论的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】轮船![]() 从某港口将一些物品送到正航行的轮船
从某港口将一些物品送到正航行的轮船![]() 上,在轮船
上,在轮船![]() 出发时,轮船
出发时,轮船![]() 位于港口
位于港口![]() 北偏西
北偏西![]() 且与
且与![]() 相距20海里的
相距20海里的![]() 处,并正以30海里的航速沿正东方向匀速行驶,假设轮船
处,并正以30海里的航速沿正东方向匀速行驶,假设轮船![]() 沿直线方向以
沿直线方向以![]() 海里/小时的航速匀速行驶,经过
海里/小时的航速匀速行驶,经过![]() 小时与轮船
小时与轮船![]() 相遇.
相遇.
(1)若使相遇时轮船![]() 航距最短,则轮船
航距最短,则轮船![]() 的航行速度大小应为多少?
的航行速度大小应为多少?
(2)假设轮船![]() 的最高航速只能达到30海里/小时,则轮船
的最高航速只能达到30海里/小时,则轮船![]() 以多大速度及什么航行方向才能在最短时间与轮船
以多大速度及什么航行方向才能在最短时间与轮船![]() 相遇,并说明理由.
相遇,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N,数列{bn}满足an=4log2bn+3,n∈N.
(1)求an,bn;
(2)求数列{anbn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com