
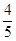 ,第二、第三种
,第二、第三种 ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为 |
 的值;
的值; .
. (2)
(2) ;
;
 表示“该公司第
表示“该公司第 种产品受欢迎”,
种产品受欢迎”, 由题意知
由题意知 由于事件“该公司至少有一种产品受欢迎”与事件“
由于事件“该公司至少有一种产品受欢迎”与事件“ ”是对立的,所以该公司至少有一种产品受欢迎的概率是
”是对立的,所以该公司至少有一种产品受欢迎的概率是

 ,整理得
,整理得 且
且 ,由
,由 ,可得
,可得
 ,进而利用期望公式得到结论。
,进而利用期望公式得到结论。 表示“该公司第
表示“该公司第 种产品受欢迎”,
种产品受欢迎”, 由题意知
由题意知 ,
, …………………………………………………………………………………………1分
…………………………………………………………………………………………1分 ”是对立的,所以该公司至少有一种产品受欢迎的概率是
”是对立的,所以该公司至少有一种产品受欢迎的概率是 ………………………………………3分
………………………………………3分
 ,整理得
,整理得 且
且 ,由
,由 ,可得
,可得 .…………………7分
.…………………7分
 ,………………………………………………9分
,………………………………………………9分 ……………………………………………………10分
……………………………………………………10分 …………………12分
…………………12分

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源:不详 题型:解答题
 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为 ,且各次投篮互不影响.(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数
,且各次投篮互不影响.(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数 的分布列与期望
的分布列与期望查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,不堵车的概率为
,不堵车的概率为 ;汽车走②号公路堵车的概率为
;汽车走②号公路堵车的概率为 ,不堵车的概率为
,不堵车的概率为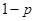 .由于客观原因甲、乙两辆汽车走①号公路,丙汽车走②号公路,且三辆车是否堵车相互之间没有影响.
.由于客观原因甲、乙两辆汽车走①号公路,丙汽车走②号公路,且三辆车是否堵车相互之间没有影响. ,求汽车走公路②堵车的概率;
,求汽车走公路②堵车的概率; 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 参加次数 | 0 | 1 | 2 | 3 |
| 人数 | 0.1 | 0.2 | 0.4 | 0.3 |
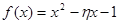 在区间
在区间 ,
, 内有零点”的事件为
内有零点”的事件为 ,求
,求 发生的概率
发生的概率 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,方差为62,则数据3x1+5,3x2+5,…,3xn+5的平均数和方差分别是( )
,方差为62,则数据3x1+5,3x2+5,…,3xn+5的平均数和方差分别是( )A. | B. |
C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com