
【题目】![]() 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E、F分别在A1B1、C1D1上,A1E=D1F=4,过点E,F的平面
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E、F分别在A1B1、C1D1上,A1E=D1F=4,过点E,F的平面![]() 与此长方体的面相交,交线围成一个正方形。
与此长方体的面相交,交线围成一个正方形。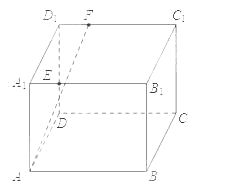
(1)(Ⅰ)在图中画出这个正方形(不必说出画法和理由);
(2)(Ⅱ)求直线AF与平面![]() 所成角的正弦值
所成角的正弦值
【答案】
(1)
交线围成的正方形EHGF如图;

(2)
【解答】作EM![]() AB,垂足为M,则AM=A1E=4,EM=AA1=8,因为EHGF为正方形,所以EH=EF=BC=10,于是MH=
AB,垂足为M,则AM=A1E=4,EM=AA1=8,因为EHGF为正方形,所以EH=EF=BC=10,于是MH=![]() ,所以AH=10,以D为坐标原点,
,所以AH=10,以D为坐标原点,![]() 的方向为x轴的正方向,建立如图所示的空间直角坐标系D-xyz,则A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8),
的方向为x轴的正方向,建立如图所示的空间直角坐标系D-xyz,则A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8),![]() =(10,0,0),
=(10,0,0),![]() =(0,-6,8),设
=(0,-6,8),设![]() =(x,y,z)是平面EHGF的法向量,则
=(x,y,z)是平面EHGF的法向量,则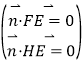 ,即
,即![]() ,所以可取
,所以可取![]() =(0,4,3)。又
=(0,4,3)。又![]() =(-10,4,8),故|cos
=(-10,4,8),故|cos![]()
![]() ,
,![]()
![]() |=
|=![]() ,所以直线AF与平面
,所以直线AF与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
【解析】根据线面平行和面面平行的性质画平面![]() 与长方体的面的交线;由交线的位置可确定公共点的位置,坐标法是求解空间角问题时常用的方法,但因其计算量大的特点很容易出错,故坐标系的选择是很重要的,便于用坐标表示相关点,先求出面
与长方体的面的交线;由交线的位置可确定公共点的位置,坐标法是求解空间角问题时常用的方法,但因其计算量大的特点很容易出错,故坐标系的选择是很重要的,便于用坐标表示相关点,先求出面![]() 的法向量,利用sin
的法向量,利用sin![]() =|cos
=|cos![]()
![]() ,
,![]()
![]() |求直线AF与平面
|求直线AF与平面![]() 所成角的正弦值.
所成角的正弦值.
【考点精析】通过灵活运用直线与平面平行的性质和空间角的异面直线所成的角,掌握一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 即可以解答此题.
即可以解答此题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D
的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D ![]() 在椭圆C上,直线l:y=kx+m与椭圆C相交于A、P两点,与x轴、y轴分别相交于点N和M,且PM=MN,点Q是点P关于x轴的对称点,QM的延长线交椭圆于点B,过点A、B分别作x轴的垂涎,垂足分别为A1、B1
在椭圆C上,直线l:y=kx+m与椭圆C相交于A、P两点,与x轴、y轴分别相交于点N和M,且PM=MN,点Q是点P关于x轴的对称点,QM的延长线交椭圆于点B,过点A、B分别作x轴的垂涎,垂足分别为A1、B1
(1)求椭圆C的方程;
(2)是否存在直线l,使得点N平分线段A1B1?若存在,求求出直线l的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于非空实数集A,定义![]() 对任意
对任意![]() .设非空实数集
.设非空实数集![]() .现给出以下命题:(1)对于任意给定符合题设条件的集合C,D,必有
.现给出以下命题:(1)对于任意给定符合题设条件的集合C,D,必有![]() ;(2)对于任意给定符合题设条件的集合C,D,必有
;(2)对于任意给定符合题设条件的集合C,D,必有![]() ;(3)对于任意给定符合题设条件的集合C,D,必有
;(3)对于任意给定符合题设条件的集合C,D,必有![]() ;(4)对于任意给定符合题设条件的集合C,D,必存在常数a,使得对任意的
;(4)对于任意给定符合题设条件的集合C,D,必存在常数a,使得对任意的![]() ,恒有
,恒有![]() .以上命题正确的个数是( )
.以上命题正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记![]() BOP=x,将动P到A、B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()
BOP=x,将动P到A、B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()
A.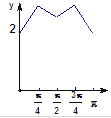
B.
C.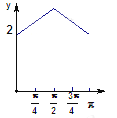
D.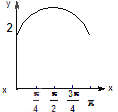
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00—10:00间各自的点击量,得如下所示的统计图,根据统计图:
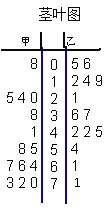
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,60]间的频率是多少?
(3)甲、乙两个网站哪个更受欢迎?并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)在直角坐标系xoy中,曲线C:y=![]() 与直线y=kx+a(a>0)交与M,N两点,
与直线y=kx+a(a>0)交与M,N两点,
(1)当k=0时,分别求C在点M和N处的切线方程;
(2)y轴上是否存在点P , 使得当k变动时,总有∠OPM=∠OPN?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)一辆小客车上有5个座位,其座位号为1,2,3,4,5,乘客P1 , P2 , P3 , P4 , P5的座位号分别为1,2,3,4,5,他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(1)(I)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
乘客 | P1 | P2 | P3 | P4 | P5 |
座位号 | 3 | 2 | 1 | 4 | 5 |
3 | 2 | 4 | 5 | 1 | |
(2)(Ⅱ)若乘客P1坐到了2号座位,其他乘客按规则就坐,求乘客P1坐到5号座位的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点。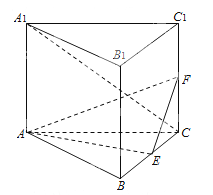
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线AC1与平面AA1BB1所成的角为45°,求三棱锥F-AEC的体积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com