
【题目】已知函数 ![]() .
.
(1)求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)单调增区间是![]() ,单调减区间是
,单调减区间是![]() ,极小值为
,极小值为![]() .(2)见解析.
.(2)见解析.
【解析】试题分析:
(1)首先对函数求导,然后结合导函数与原函数的单调性可得函数的单调增区间是![]() ,单调减区间是
,单调减区间是![]() ,极小值为
,极小值为![]()
(2)由题意结合(1)的结论分类讨论可得不存在满足题意的实数a.
试题解析:
由题意知, ![]() .
.
(1)由![]() 得
得![]() ,解得
,解得![]() ,所以函数
,所以函数![]() 的单调增区间是
的单调增区间是![]() ;
;
由![]() 得
得![]() ,解得
,解得![]() ,所以函数
,所以函数![]() 的单调减区间是
的单调减区间是![]() .
.![]() 当
当![]() 时,函数
时,函数![]() 有极小值为
有极小值为![]() .
.
(2)由(1)可知,当![]() 时,
时, ![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() 单调递增.
单调递增.
①若![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上为增函数,故函数
上为增函数,故函数![]() 的最小值为
的最小值为![]() ,显然
,显然![]() ,故不满足条件.
,故不满足条件.
②若![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,故函数
上为增函数,故函数![]() 的最小值为
的最小值为![]() ,即
,即![]() ,解得
,解得![]() ,而
,而![]() ,故不满足条件.
,故不满足条件.
③若![]() ,即
,即![]() 时,函数
时,函数![]() 在在
在在![]() 上为减函数,故函数
上为减函数,故函数![]() 的最小值为
的最小值为![]() ,即
,即![]() ,而
,而![]() 不满足条件,综上所述,这样的
不满足条件,综上所述,这样的![]() 不存在.
不存在.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 与底面
与底面![]() 垂直,
垂直, ![]() 为正三角形,
为正三角形, ![]() ,
, ![]() ,点
,点![]() 分别为线段
分别为线段![]() 的中点,
的中点, ![]() 分别为线段
分别为线段![]() 上一点,且
上一点,且![]() ,
, ![]() .
.
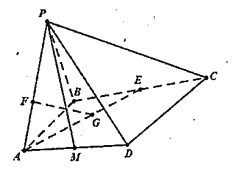
(1)当![]() 时,求证:
时,求证: ![]() 平面
平面![]() ;
;
(2)试问:直线![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,若存在,求
,若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了![]() 名女性或
名女性或![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.

(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限接近圆的面积,并创立了“割圆术”,利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”,利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )
(参考数据: ![]() )
)
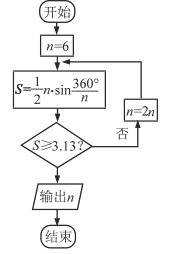
A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】班主任为了对本班学生的考试成绩进行分析,决定从全班![]() 位女同学,
位女同学, ![]() 位男同学中随机
位男同学中随机
抽取一个容量为![]() 的样本进行分析.
的样本进行分析.
(Ⅰ)如果按性别比例分层抽样,求样本中男生、女生人数分别是多少;
(Ⅱ)随机抽取![]() 位同学,数学成绩由低到高依次为:
位同学,数学成绩由低到高依次为: ![]() ;物理成绩由低到高依次为:
;物理成绩由低到高依次为: ![]() ,若规定
,若规定![]() 分(含
分(含![]() 分)以上为优秀,记
分)以上为优秀,记![]() 为这
为这![]() 位同学中数学和物理分数均为优秀的人数,求
位同学中数学和物理分数均为优秀的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将7名应届师范大学毕业生分配到3所中学任教.
(1)4个人分到甲学校,2个人分到乙学校,1个人分到丙学校,有多少种不同的分配方案?
(2)一所学校去4个人,另一所学校去2个人,剩下的一个学校去1个人,有多少种不同的分配方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com