
【题目】已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.
【答案】(1)选择函数模型![]() ,函数解析式为
,函数解析式为![]() ;(2)以1百公里/小时航行时可使AB段的航行费用最少,且最少航行费用为2.1万元.
;(2)以1百公里/小时航行时可使AB段的航行费用最少,且最少航行费用为2.1万元.
【解析】
(1)对题中所给的三个函数解析式进行分析,对应其性质,结合题中所给的条件,作出正确的选择,之后利用待定系数法求得解析式,得出结果;
(2)根据题意,列出函数解析式,之后应用配方法求得最值,得到结果.
(1)若选择函数模型![]() ,则该函数在
,则该函数在![]() 上为单调减函数,
上为单调减函数,
这与试验数据相矛盾,所以不选择该函数模型.
若选择函数模型![]() ,须
,须![]() ,这与试验数据在
,这与试验数据在![]() 时有意义矛盾,
时有意义矛盾,
所以不选择该函数模型.
从而只能选择函数模型![]() ,由试验数据得,
,由试验数据得,
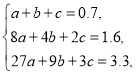 ,即
,即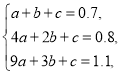 ,解得
,解得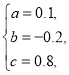
故所求函数解析式为:![]() .
.
(2)设超级快艇在AB段的航行费用为y(万元),
则所需时间为![]() (小时),其中
(小时),其中![]() ,
,
结合(1)知,![]()
![]()
所以当![]() 时,
时,![]() .
.
答:当该超级快艇以1百公里/小时航行时可使AB段的航行费用最少,且最少航行费用为2.1万元.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,解不等式
,解不等式![]() ;
;
(Ⅱ)设![]() 是函数
是函数![]() 的四个不同的零点,问是否存在实数
的四个不同的零点,问是否存在实数![]() ,使得其中三个零点成等差数列?若存在,求出所有
,使得其中三个零点成等差数列?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 且函数
且函数![]() 图象上点
图象上点![]() 处的切线斜率为
处的切线斜率为![]() .
.
(1)试用含有![]() 的式子表示
的式子表示![]() ,并讨论
,并讨论![]() 的单调性;
的单调性;
(2)对于函数图象上的不同两点![]() 如果在函数图象上存在点
如果在函数图象上存在点![]() 使得点
使得点![]() 处的切线
处的切线![]() ,则称
,则称![]() 存在“跟随切线”.特别地,当
存在“跟随切线”.特别地,当![]() 时,又称
时,又称![]() 存在“中值跟随切线”.试问:函数
存在“中值跟随切线”.试问:函数![]() 上是否存在两点
上是否存在两点![]() 使得它存在“中值跟随切线”,若存在,求出
使得它存在“中值跟随切线”,若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD﹣A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1= ![]() ,∠BAD=120°.
,∠BAD=120°.
(Ⅰ)求异面直线A1B与AC1所成角的余弦值;
(Ⅱ)求二面角B﹣A1D﹣A的正弦值.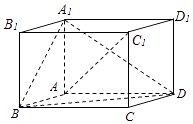
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com