
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.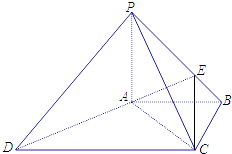
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC.
【答案】
(1)解:∵PA⊥底面ABCD,BC底面ABCD,∴PA⊥BC,
又∵AB⊥BC,PA∩AB=A,∴BC⊥平面PAB.
∵BC平面PCB,∴平面PAB⊥平面PCB.
(2)∵PA⊥底面ABCD,∴AC为PC在平面ABCD内的射影.
又∵PC⊥AD,∴AC⊥AD.
在梯形ABCD中,由AB⊥BC,AB=BC,得 ![]() ,
,
∴ ![]() .
.
又∵AC⊥AD,故△DAC为等腰直角三角形.
∴ ![]() .
.
连接BD,交AC于点M,则由AB∥CD得: ![]() .
.
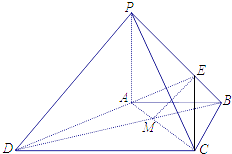
在△BPD中, ![]() ,所以PD∥EM
,所以PD∥EM
又∵PD平面EAC,EM平面EAC,
∴PD∥平面EAC.
【解析】1、由线面垂直得到线线垂直,再由线线垂直得到线面垂直,根据线线垂直的判定定理可得证。
2、做辅助线连接BD,交AC于点M,连接EM由射影定理可得AC⊥AD. 在梯形ABCD中,由AB⊥BC,AB=BC,得 ∠ D C A = ∠ B A C = ![]() ,∵AC⊥AD,故△DAC为等腰直角三角形. D C =
,∵AC⊥AD,故△DAC为等腰直角三角形. D C = ![]() A C =
A C = ![]() (
( ![]() A B ) = 2 A B ,由AB∥CD得
A B ) = 2 A B ,由AB∥CD得 ![]() ,在△BPD中,
,在△BPD中, ![]() ,所以PD∥EM,又∵PD平面EAC,EM平面EAC,∴PD∥平面EAC.
,所以PD∥EM,又∵PD平面EAC,EM平面EAC,∴PD∥平面EAC.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=mlnx(m∈R),g(x)=cosx.
(1)若函数 ![]() 在(1,+∞)上单调递增,求m的取值范围;
在(1,+∞)上单调递增,求m的取值范围;
(2)设函数φ(x)=f(x)+g(x),若对任意的 ![]() ,都有φ(x)≥0,求m的取值范围;
,都有φ(x)≥0,求m的取值范围;
(3)设m>0,点P(x0 , y0)是函数f(x)与g(x)的一个交点,且函数f(x)与g(x)在点P处的切线互相垂直,求证:存在唯一的x0满足题意,且 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,点列Pn(n=1,2,…)在△ABC内部,且△PnAB与△PnAC的面积比为2:1,若对n∈N*都存在数列{bn}满足 ![]() ,则a4的值为 .
,则a4的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘成折线图如下:
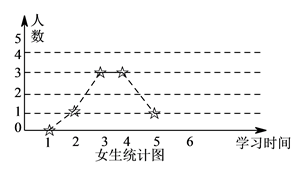
(I)已知该校有 ![]() 名学生,试估计全校学生中,每天学习不足
名学生,试估计全校学生中,每天学习不足 ![]() 小时的人数.
小时的人数.
(II)若从学习时间不少于 ![]() 小时的学生中选取
小时的学生中选取 ![]() 人,设选到的男生人数为
人,设选到的男生人数为 ![]() ,求随机变量
,求随机变量 ![]() 的分布列.
的分布列.
(III)试比较男生学习时间的方差 ![]() 与女生学习时间方差
与女生学习时间方差 ![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知(2x﹣ ![]() )5(Ⅰ)求展开式中含
)5(Ⅰ)求展开式中含 ![]() 项的系数
项的系数
(Ⅱ)设(2x﹣ ![]() )5的展开式中前三项的二项式系数之和为M,(1+ax)6的展开式中各项系数之和为N,若4M=N,求实数a的值.
)5的展开式中前三项的二项式系数之和为M,(1+ax)6的展开式中各项系数之和为N,若4M=N,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学开设甲、乙、丙三门选修课供学生任意选修(也可不选),假设学生是否选修哪门课彼此互不影响.已知某学生只选修甲一门课的概率为0.08,选修甲和乙两门课的概率为0.12,至少选修一门的概率是0.88.
(1)求该学生选修甲、乙、丙的概率分别是多少?
(2)用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数λ>0,设函数f(x)=eλx﹣ ![]() .
.
(Ⅰ)当λ=1时,求函数g(x)=f(x)+lnx﹣x的极值;
(Ⅱ)若对任意x∈(0,+∞),不等式f(x)≥0恒成立,求λ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com