
分析 (Ⅰ)利用绝对值不等式的几何意义求解即可.
(Ⅱ)去掉绝对值符号,利用数形结合,以及直线系方程,转化求解即可.
解答 (本小题满分10分)
解:(Ⅰ)由不等式的性质可得:|2x+1|+|2x-2|≥|2x+1-2x+2|=3,
所以当且仅当$-\frac{1}{2}≤x≤1$时,函数f(x)的最小值为3.…(5分)
(Ⅱ)$f(x)=|{2x+1}|+|{2x-2}|=\left\{\begin{array}{l}4x-1({x≥1})\\ 3({-\frac{1}{2}<x<1})\\ 1-4x({x≤-\frac{1}{2},})\end{array}\right.$…(7分)
又函数y=ax+1恒过定点(0,1),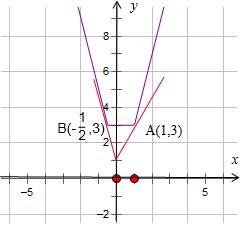
结合函数图象可得:a<-4或a>2.…(10分)
点评 本题考查函数的最值的求法,数形结合的应用,直线系方程的应用,绝对值不等式的几何意义,考查计算能力.


科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:解答题
已知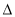 ABC的三边为a,b,c.其面积S=
ABC的三边为a,b,c.其面积S= 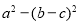 ,且b+c=8.
,且b+c=8.
(1)求cosA
(2)求S的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:解答题
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段: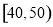 ,
,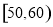 ,…,
,…,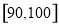 后得到如下频率分布直方图.
后得到如下频率分布直方图.
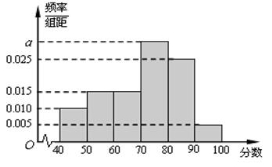
(Ⅰ)求分数在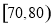 内的频率;
内的频率;
(Ⅱ)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数;(小数点后保留一位有效数字)
(Ⅲ)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p:4+4=9,q:7>4 | B. | p:a∈{a,b,c},q:{a}⊆{a,b,c} | ||
| C. | p:15是质数,q:8是12的约数 | D. | p:2是偶数,q:2不是质数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{18}-\frac{y^2}{32}=1$ | C. | $\frac{x^2}{9}-\frac{y^2}{25}=1$ | D. | $\frac{x^2}{36}-\frac{y^2}{64}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
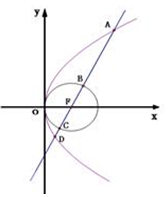 圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点
圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com