
【题目】四色猜想是近代数学难题之一,四色猜想的内容是:“任何一张地图最多用四种颜色就能使具有共同边界的国家着上不同的颜色”,如图,一张地图被分成了五个区域,每个区域只使用一种颜色,现有4种颜色可供选择(四种颜色不一定用完),则满足四色猜想的不同涂色种数为__________

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为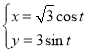 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线l和曲线![]() 的直角坐标方程,曲线
的直角坐标方程,曲线![]() 的普通方程;
的普通方程;
(2)若直线l与曲线![]() 和曲线
和曲线![]() 在第一象限的交点分别为P,Q,求
在第一象限的交点分别为P,Q,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2019个数是( )
A. 3972 B. 3974 C. 3991 D. 3993
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校自主招生一次面试成绩的茎叶图和频率分布直方图均收到了不同程度的损坏,其可见部分信息如下,据此解答下列问题:
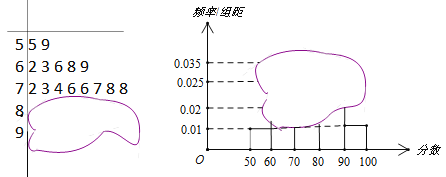
(1)求参加此次高校自主招生面试的总人数![]() 、面试成绩的中位数及分数在
、面试成绩的中位数及分数在![]() 内的人数;
内的人数;
(2)若从面试成绩在![]() 内的学生中任选三人进行随机复查,求恰好有二人分数在
内的学生中任选三人进行随机复查,求恰好有二人分数在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com