
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴,且f(x)在(
为y=f(x)图象的对称轴,且f(x)在( ![]() ,
, ![]() )上单调,则ω的最大值为( )
)上单调,则ω的最大值为( )
A.11
B.9
C.7
D.5
【答案】B
【解析】解:∵x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴, ∴
为y=f(x)图象的对称轴, ∴ ![]() ,即
,即 ![]() ,(n∈N)
,(n∈N)
即ω=2n+1,(n∈N)
即ω为正奇数,
∵f(x)在( ![]() ,
, ![]() )上单调,则
)上单调,则 ![]() ﹣
﹣ ![]() =
= ![]() ≤
≤ ![]() ,
,
即T= ![]() ≥
≥ ![]() ,解得:ω≤12,
,解得:ω≤12,
当ω=11时,﹣ ![]() +φ=kπ,k∈Z,
+φ=kπ,k∈Z,
∵|φ|≤ ![]() ,
,
∴φ=﹣ ![]() ,
,
此时f(x)在( ![]() ,
, ![]() )不单调,不满足题意;
)不单调,不满足题意;
当ω=9时,﹣ ![]() +φ=kπ,k∈Z,
+φ=kπ,k∈Z,
∵|φ|≤ ![]() ,
,
∴φ= ![]() ,
,
此时f(x)在( ![]() ,
, ![]() )单调,满足题意;
)单调,满足题意;
故ω的最大值为9,
故选:B
根据已知可得ω为正奇数,且ω≤12,结合x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴,求出满足条件的解析式,并结合f(x)在(
为y=f(x)图象的对称轴,求出满足条件的解析式,并结合f(x)在( ![]() ,
, ![]() )上单调,可得ω的最大值.
)上单调,可得ω的最大值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos( ![]() ﹣x)cos(x+
﹣x)cos(x+ ![]() )+
)+ ![]() . (Ⅰ)求函数f(x)的最小正周期和单调递减区间;
. (Ⅰ)求函数f(x)的最小正周期和单调递减区间;
(Ⅱ)求函数f(x)在区间[0, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值ξ(元)的概率分布列和期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mln(x+1),g(x)= ![]() (x>﹣1).
(x>﹣1).
(Ⅰ)讨论函数F(x)=f(x)﹣g(x)在(﹣1,+∞)上的单调性;
(Ⅱ)若y=f(x)与y=g(x)的图象有且仅有一条公切线,试求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
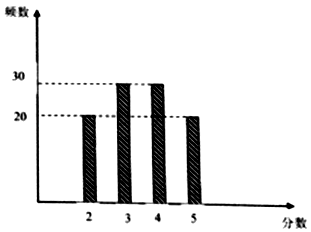
【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.
(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;
(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).
(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).
服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
等级 | 不好 | 较好 | 优良 |
奖惩标准(元) | ﹣1000 | 2000 | 3000 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系xoy中,曲线C1的参数方程为 ![]() (β为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4cosθ.
(β为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4cosθ.
(Ⅰ)将曲线C1的方程化为极坐标方程;
(Ⅱ)已知直线l的参数方程为 ![]() (
( ![]() <α<π,t为参数,t≠0),l与C1交与点A,l与C2交与点B,且|AB|=
<α<π,t为参数,t≠0),l与C1交与点A,l与C2交与点B,且|AB|= ![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x﹣ ![]() )+2cos2x,将函数y=f(x)的图象向右平移
)+2cos2x,将函数y=f(x)的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
A.(﹣ ![]() ,1)
,1)
B.(﹣ ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1 , 则双曲线的离心率为( )
A.![]()
B.![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com