已知函数f(x)=xlnx,g(x)=x3+mx2-nx(m,n为实数).
(1)若x=1是函数y=g(x)的一个极值点,求m与n的关系式;
(2)在(1)的条件下,求函数g(x)的单调递增区间;
(3)若关于x的不等式2f(x)≤g'(x)+1+n的解集为P,且(0,+∞)⊆P,求实数m的取值范围.
解:(1)g'(x)=3x
2+2mx-n,
由题意得
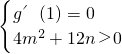
,∴n=2m+3(m≠-3).
(2)由(1)知:g'(x)=3x
2+2mx-(2m+3)=(x-1)[3x+(2m+3)],
令g'(x)=0,得
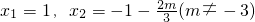
①当
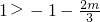
,即m>-3时,由g'(x)>0得
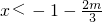
或x>1,
∴g(x)的单调递增区间是
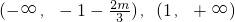
;
②当
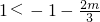
,即m<-3时,由g'(x)>0得x<1或
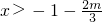
,
∴g(x)的单调递增区间是

.
(3)由(0,+∞)⊆P得2f(x)≤g'(x)+1+n在x∈(0,+∞)上恒成立,
即:2xlnx≤3x
2+2mx+1在x∈(0,+∞)上恒成立,
可得
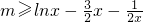
在x∈(0,+∞)上恒成立,
设
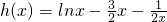
,
则
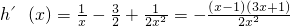
,
令h'(x)=0,得

(舍),
∵当0<x<1时,h'(x)>0,h(x)在(0,1)上单调递增;
当x>1时,h'(x)<0,h(x)在(1,+∞)上单调递减,
∴当x=1时,h(x)取得最大值,h(x)
max=-2,
∴m≥-2,即m的取值范围是[-2,+∞)
分析:(1)由函数极值的定义,先求函数g(x)=x
3+mx
2-nx的导函数,由
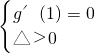
可得m与n的关系式
(2)在(1)的条件下g'(x)=3x
2+2mx-(2m+3)=(x-1)[3x+(2m+3)],解不等式g'(x)>0,即可得函数g(x)的单调递增区间,但需要比较根1与
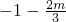
的大小,因此需讨论后得结果
(3)由(0,+∞)⊆P得2f(x)≤g'(x)+1+n在x∈(0,+∞)上恒成立,参变分离后可转化为
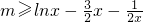
在x∈(0,+∞)上恒成立,从而只需求
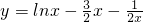
的最大值即可,利用导数判断其单调性可得结果
点评:本题综合考查了导数在函数极值、单调性、最值中的应用,解题时要认真体会导数在研究函数性质方面的积极作用,规范解题,还要注意运算技巧和分类讨论

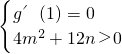 ,∴n=2m+3(m≠-3).
,∴n=2m+3(m≠-3).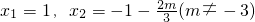
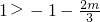 ,即m>-3时,由g'(x)>0得
,即m>-3时,由g'(x)>0得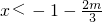 或x>1,
或x>1,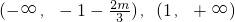 ;
; 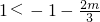 ,即m<-3时,由g'(x)>0得x<1或
,即m<-3时,由g'(x)>0得x<1或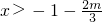 ,
, .
.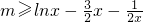 在x∈(0,+∞)上恒成立,
在x∈(0,+∞)上恒成立,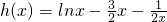 ,
,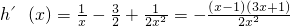 ,
, (舍),
(舍),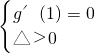 可得m与n的关系式
可得m与n的关系式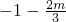 的大小,因此需讨论后得结果
的大小,因此需讨论后得结果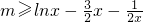 在x∈(0,+∞)上恒成立,从而只需求
在x∈(0,+∞)上恒成立,从而只需求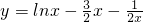 的最大值即可,利用导数判断其单调性可得结果
的最大值即可,利用导数判断其单调性可得结果

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<