
����Ŀ�����������ֻ��ķ�չ����Խ��Խ��Ϊ���ǽ�����һ�ַ�ʽ��ij������ʹ���Ž�����̬�Ƚ��е��飬��������� 50 �ˣ����������Ƶ���ֲ�����ʹ���Ž��������������
���䣨�꣩ | [15��25�� | [25��35�� | [35��45�� | [45��55�� | [55��65�� | [65��75�� |
Ƶ�� | 5 | 10 | 15 | 10 | 5 | 5 |
������ | 5 | 10 | 12 | 7 | 2 | 1 |
��I��������ͳ��������д���� 2��2 �����������ж��Ƿ���99%�İ�����Ϊ����45��Ϊ�ֽ���ʹ���Ž�����̬���в��죻
���䲻����45����� | �������45����� | �ϼ� | |
�� | |||
���� | |||
�ϼ� |
��������������[55��65����[65��75���ı��������������ȡ���˽����ٵ��飬��ѡ�е�4������ʹ���Ž���������ΪX�����������X�ķֲ��к���ѧ����
�ο���ʽ��K2= ![]() ������n=a+b+c+d
������n=a+b+c+d
�ο����ݣ�
P��K2��k0�� | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
���𰸡��⣺��I��������ͳ��������д���� 2��2 �����������£�
���䲻����45����� | �������45����� | �ϼ� | |
�� | 10 | 27 | 37 |
���� | 10 | 3 | 13 |
�ϼ� | 20 | 30 | 50 |
���ݹ�ʽ����K2= ![]() =
= ![]() ��9.98��6.635��
��9.98��6.635��
������99%�İ�����Ϊ����45��Ϊ�ֽ���ʹ���Ž�����̬���в��죻
���������⣬X�����п���ȡֵΪ0��1��2��3��
��P��X=0��= ![]()
![]() =
= ![]() ��
�� ![]() =
= ![]() ��
��
P��X=1��= ![]()
![]() +
+ ![]()
![]() =
= ![]() ��
�� ![]() +
+ ![]() ��
�� ![]() =
= ![]() ��
��
P��X=2��= ![]()
![]() +
+ ![]()
![]() =
= ![]() ��
�� ![]() +
+ ![]() ��
�� ![]() =
= ![]() ��
��
P��X=3��= ![]()
![]() =
= ![]() ��
�� ![]() =
= ![]() ��
��
�������X�ķֲ���Ϊ��
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
����X����ѧ����ΪEX=0�� ![]() +1��
+1�� ![]() +2��
+2�� ![]() +3��
+3�� ![]() =
= ![]() =
= ![]()
����������I��������Ŀ�е�������д�����������ù�ʽ����K2�������������ɵó����ۣ�����������ó�X�����п���ȡֵ�������Ӧ�ĸ���ֵ��д��X�ķֲ�������ѧ����ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=m6x��4x �� m��R��
��1����m= ![]() ʱ��������f��x+1����f��x����ʵ��x�ķ�Χ��
ʱ��������f��x+1����f��x����ʵ��x�ķ�Χ��
��2����f��x����9x�������x��R���������ʵ��m�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯�� ![]() �Ķ�����Ϊ
�Ķ�����Ϊ ![]() ����������
���������� ![]() ����
���� ![]() ����
���� ![]() ʱ��
ʱ�� ![]() .
.
��1���� ![]() ��ֵ��
��ֵ��
��2���жϺ��� ![]() ����ż�ԣ�
����ż�ԣ�
��3����� ![]() ����
���� ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax��lnx��1��
��1��������f��x��������[1��+�ޣ��ϵ�������ʵ��a��ȡֵ��Χ��
��2����֤�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������1���ࡢ��2�������49��ѧ����������һ����ѧ�����еijɼ�ͳ�����±���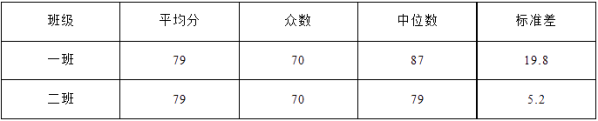
��1������������һ�λ������Ҫ������
��һ(1)���С�ջؼҶ�����˵�����������ѧ���飬ȫ��ƽ����Ϊ79�֣���70�ֵ�����࣬�ҵ���85�֣��ڰ������������ˣ���
��2��������ݱ��е����ݣ��������������ѧ����������м�Ҫ��������������飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=x2+bln��x+1��������b��0��
��1����b=1ʱ��������y=f��x���ڵ㣨0��0���������߷��̣�
��2�����ۺ���f��x���ĵ����ԣ�
��3����n��N* �� ��n��2ʱ֤������ʽ��ln[�� ![]() +1����
+1���� ![]() +1������
+1������ ![]() +1��]+
+1��]+ ![]() +
+ ![]() +��+
+��+ ![]() ��
�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A��BCD��AB=AC=1��DB=DC=2��AD=BC= ![]() ��������A��BCD�������ı����Ϊ�� ��
��������A��BCD�������ı����Ϊ�� ��
A.��
B.![]()
C.4��
D.7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʾ����飬ij��ѧ������Ӱ�ֱ�ִ��ϲ��������ϲ�����͡�һ�㡱����̬�ȣ�����ִ��һ�㡱̬�ȵıȡ���ϲ�����Ķ�12�ˣ����ֲ����������ȫ��ѡ������ѧ����̸��Ӱ�����ѡ������5λ��ϲ������Ӱ��ͬѧ��1λ����ϲ������Ӱ��ͬѧ��3λִ��һ�㡱̬�ȵ�ͬѧ����ȫ��ѧ���С�ϲ������Ӱ�ı�ȫ��ѧ��������һ�뻹����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com