
| 8 |
| 7 |
| 1 |
| 7 |
|
| 2 |
| 1 |
| 4 |
| p |
| q |
| 2 |
| 2 |
| 1 |
| a1 |
| 1 | ||
|
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| a |
-1+
| ||
| 2 |
| pn |
| qn |
| 2 |
| 2 |
| 1 |
| a1 |
| 1 | ||
|
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a1 |
| 1 |
| a |
| 1 |
| a |
-1+
| ||
| 2 |
-1-
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a1 |
| 1 |
| a |
| 1 |
| a |
-2+
| ||
| 2 |
| 2 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| a1 |
| 1 |
| a |
| 1 |
| a |
-3+
| ||
| 2 |
-3-
| ||
| 2 |
-1+
| ||
| 2 |
| 2 |
-3+
| ||
| 2 |
| pn |
| qn |
| pn |
| qn |
| p |
| q |
| p1 |
| q1 |
| qn |
| pn |
| ¶¬ |
| pn |
| pn |
| qn |
| 1 |
| an |
| qn |
| pn |
| 1 |
| an |
| ¶¬ |
| pn |


 Ω×ߡ∑–¬Õ¨≤Ω¡∑œ∞œµ¡–¥∞∏
Ω×ߡ∑–¬Õ¨≤Ω¡∑œ∞œµ¡–¥∞∏ øŒ«∞øŒ∫ÛÕ¨≤Ω¡∑œ∞œµ¡–¥∞∏
øŒ«∞øŒ∫ÛÕ¨≤Ω¡∑œ∞œµ¡–¥∞∏ øŒÃ√–°◊˜“µœµ¡–¥∞∏
øŒÃ√–°◊˜“µœµ¡–¥∞∏ ª∆∏‘–°◊¥‘™ø⁄À„ÀŸÀ„¡∑œ∞≤·œµ¡–¥∞∏
ª∆∏‘–°◊¥‘™ø⁄À„ÀŸÀ„¡∑œ∞≤·œµ¡–¥∞∏ ≥…π¶—µ¡∑º∆ªÆœµ¡–¥∞∏
≥…π¶—µ¡∑º∆ªÆœµ¡–¥∞∏ ±∂ÀŸ—µ¡∑∑®÷±Õ®÷–øºøºµ„œµ¡–¥∞∏
±∂ÀŸ—µ¡∑∑®÷±Õ®÷–øºøºµ„œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 8 |
| 7 |
| 1 |
| 7 |
|
| 2 |
| 1 |
| 4 |
| p |
| q |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
|
| 2 |
| 1 |
| 4 |
| p |
| q |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
|
| 1 |
| 2 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫2013ƒÍ…œ∫£ –—Ó∆÷«¯∏þøº ˝—ß“ªƒ£ ‘æÌ£®¿Ìø∆£©£®Ω‚Œˆ∞Ê£© –գ∫Ω‚¥Ã‚
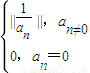 ∆‰÷–n=1£¨2£¨3£¨°≠
∆‰÷–n=1£¨2£¨3£¨°≠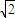 £¨«Û ˝¡–{an}£ª
£¨«Û ˝¡–{an}£ª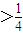 ±£¨∂‘»Œ“‚µƒn° N*£¨∂º”–an=a£¨«Û∑˚∫œ“™«Ûµƒ µ ˝aππ≥…µƒºØ∫œA£Æ
±£¨∂‘»Œ“‚µƒn° N*£¨∂º”–an=a£¨«Û∑˚∫œ“™«Ûµƒ µ ˝aππ≥…µƒºØ∫œA£Æ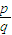 £®p «’˚ ˝£¨q «’˝’˚ ˝£¨p°¢qª•÷ £©£¨Œ ∂‘”⁄¥Û”⁄qµƒ»Œ“‚’˝’˚ ˝n£¨ «∑Ò∂º”–an=0≥…¡¢£¨≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
£®p «’˚ ˝£¨q «’˝’˚ ˝£¨p°¢qª•÷ £©£¨Œ ∂‘”⁄¥Û”⁄qµƒ»Œ“‚’˝’˚ ˝n£¨ «∑Ò∂º”–an=0≥…¡¢£¨≤¢÷§√˜ƒ„µƒΩ·¬€£Æ≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com