[题目]解不等式: ≥2．题目和参考答案——青夏教育精英家教网—

【题目】解不等式： ≥2．

【答案】解：不等式移项得： ﹣2≥0，变形得： ≤0，
即2（x﹣ ）（x﹣6）（x﹣3）（x﹣5）≤0，且x≠3，x≠5，
根据题意画出图形，如图所示：

根据图形得： ≤x＜3或5＜x≤6，
则原不等式的解集为[ ，3）∪（5，6]．
【解析】把不等式的右边移项到左边，通分后把分子分母都分解因式，得到的式子小于等于0，然后根据题意画出图形，在数轴上即可得到原不等式的解集．
【考点精析】根据题目的已知条件，利用解一元二次不等式的相关知识可以得到问题的答案，需要掌握求一元二次不等式解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边．

练习册系列答案

150加50篇英语完形填空与阅读理解系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥中，底面是梯形，，，，，侧面底面.

（1）求证：平面平面；

（2）若，且三棱锥的体积为，求侧面的面积.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知在平面直角坐标系中，为坐标原点，曲线：（为参数），在以平面直角坐标系的原点为极点，轴的正半轴为极轴，有相同单位长度的极坐标系中，直线： .

(Ⅰ)求曲线的普通方程和直线的直角坐标方程；

(Ⅱ)求与直线平行且与曲线相切的直线的直角坐标方程。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知 =（ sinx，m+cosx）， =（cosx，﹣m+cosx），且f（x）=
（1）求函数f（x）的解析式；
（2）当x∈ 时，f（x）的最小值是﹣4，求此时函数f（x）的最大值，并求出相应的x的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了了解甲、乙两个工厂生产的轮胎的宽度是否达标，分别从两厂随机各选取了10个轮胎，将每个轮胎的宽度（单位：mm）记录下来并绘制出如下的折线图：

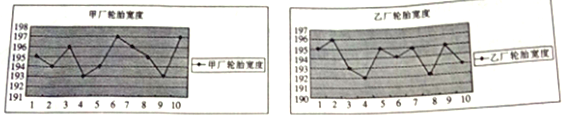
（1）分别计算甲、乙两厂提供的10个轮胎宽度的平均值；

（2）轮胎的宽度在内，则称这个轮胎是标准轮胎.试比较甲、乙两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小，根据两厂的标准轮胎宽度的平均水平及其波动情况，判断这两个工厂哪个厂的轮胎相对更好？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】原命题：“，为两个实数，若，则，中至少有一个不小于1”，下列说法错误的是（）

A. 逆命题为：若，中至少有一个不小于1，则，为假命题

B. 否命题为：若，则，都小于1，为假命题

C. 逆否命题为：若，都小于1，则，为真命题

D. “”是“，中至少有一个不小于1”的必要不充分条件

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某学校为调查高一新生上学路程所需要的时间（单位：分钟），从高一年级新生中随机抽取100名新生按上学所需时间分组：第1组（0，10]，第2组（10，20]，第3组（20，30]，第4组（30，40]，第5组（40，50]，得到的频率分布直方图如图所示．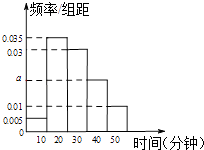

（1）根据图中数据求a的值；
（2）若从第3，4，5组中用分层抽样的方法抽取6名新生参与交通安全问卷调查，应从第3，4，5组各抽取多少名新生？
（3）在（2）的条件下，该校决定从这6名新生中随机抽取2名新生参加交通安全宣传活动，求第4组至少有一名志愿者被抽中的概率．