
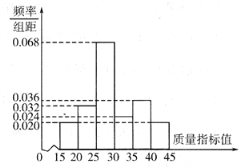
【题目】某地方政府召开全面展开新旧动能转换重大工程动员大会,动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前、后生产的大量产品中各抽取了200件作为样本,检测一项质量指标值.若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.如图所示的是设备改造前样本的频率分布直方图.
内的产品视为合格品,否则为不合格品.如图所示的是设备改造前样本的频率分布直方图.
(1)若设备改造后样本的该项质量指标值服从正态分布![]() ,求改造后样本中不合格品的件数;
,求改造后样本中不合格品的件数;
(2)完成下面2×2列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量标值与设备改造有关.
0 | 设备改造前 | 设备改造后 | 合计 |
合格品件数 | |||
不合格品件数 | |||
合计 |
附参考公式和数据:
若![]() ,则
,则![]() ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)10;(2)列联表见解析,有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关.
【解析】
(1)设备改造后该项质量指标服从正态分布![]() ,得
,得![]() ,
,![]() ,然后
,然后![]() ,然后即可求出
,然后即可求出
(2)由设备改造前样本的频率分布直方图,可知不合格频数为![]() ,然后填表,再算出
,然后填表,再算出![]() 即可
即可
解:(1)∵设备改造后该项质量指标服从正态分布![]() ,
,
得![]() ,
,![]() ,
,
又∵![]() ,
,
∴设备改造后不合格的样本数为![]() .
.
(2)由设备改造前样本的频率分布直方图,可知不合格频数为
![]() .
.
得2×2列联表如下
设备改造前 | 设备改造后 | 合计 | |
合格品 | 160 | 190 | 350 |
不合格品 | 40 | 10 | 50 |
合计 | 200 | 200 | 400 |
![]() ,
,
∴有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() 表示的曲线为
表示的曲线为![]() 的图象,对于函数
的图象,对于函数![]() 有如下结论:①
有如下结论:①![]() 在
在![]() 上单调递减;②函数
上单调递减;②函数![]() 至少存在一个零点;③
至少存在一个零点;③![]() 的最大值为
的最大值为![]() ;④若函数
;④若函数![]() 和
和![]() 图象关于原点对称,则
图象关于原点对称,则![]() 由方程
由方程![]() 所确定;则正确命题序号为( )
所确定;则正确命题序号为( )
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的100人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 10 | 7 | 13 |
(1)若规定问卷得分不低于70分的市民称为“环保关注者”,请完成答题卡中的![]() 列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.视频率为概率.
①在我市所有“环保达人”中,随机抽取3人,求抽取的3人中,既有男“环保达人”又有女“环保达人”的概率;
②为了鼓励市民关注环保,针对此次的调查制定了如下奖励方案:“环保达人”获得两次抽奖活动;其他参与的市民获得一次抽奖活动.每次抽奖获得红包的金额和对应的概率.如下表:
红包金额(单位:元) | 10 | 20 |
概率 |
|
|
现某市民要参加此次问卷调查,记![]() (单位:元)为该市民参加间卷调查获得的红包金额,求
(单位:元)为该市民参加间卷调查获得的红包金额,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列{an}的前n项和为Sn,满足:对任意的n∈N*,都有an+1+Sn+1=1,又a1![]() .
.
(1)求数列{an}的通项公式;
(2)令bn=log2an,求![]() (n∈N*)
(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①在回归分析模型中,残差平方和越大,说明模型的拟合效果越好;
②某学校有男教师60名、女教师40名,为了解教师的体育爱好情况,在全体教师中抽取20名调查,则宜采用的抽样方法是分层抽样;
③线性相关系数![]() 越大,两个变量的线性相关性越弱;反之,线性相关性越强;
越大,两个变量的线性相关性越弱;反之,线性相关性越强;
④在回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 增加0.5个单位.
增加0.5个单位.
其中正确的结论是( )
A. ①②B. ①④
C. ②③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为矩形,AB=![]() ,BC=1,E,F分别是AB,PC的中点,DE⊥PA.
,BC=1,E,F分别是AB,PC的中点,DE⊥PA.
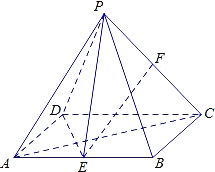
(1)求证:EF∥平面PAD;
(2)求证:平面PAC⊥平面PDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC — A1B1C1中,AB=AC,BB1=BC,点P,Q,R分别是棱BC,CC1,B1C1的中点.
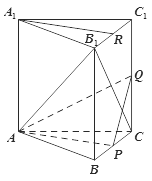
(1)求证:A1R//平面APQ;
(2)求证:直线B1C⊥平面APQ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com