
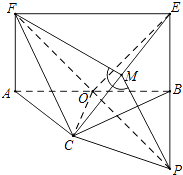
【题目】在如图的平面多边形ACBEF中,四边形ABEF是矩形,点O为AB的中点,△ABC中,AC=BC,现沿着AB将△ABC折起,直至平面ABEF⊥平面ABC,如图,此时OE⊥FC. 
(1)求证:OF⊥EC;
(2)若FC与平面ABC所成角为30°,求二面角F﹣CE﹣B的余弦值.
【答案】
(1)证明:连结OC,∵AC=BC,O是AB的中点,故OC⊥AB.
又∵平面ABC⊥平面ABEF,
故OC⊥平面ABE,
于是OC⊥OF.OC⊥OE,
又OE⊥FC,
∵OF⊥平面OFC,
∴OE⊥OF,
又∵OC⊥OF,∴OF⊥平面OEC,
∴OF⊥EC.
(2)由(I)得AB=2AF.不妨设AF=1,AB=2.
∵∠FCA为直线FC与平面ABC所成的角,
∴∠FCA=30°,
∴FC=EC=2,△EFC为等边三角形.
设FO∩EB=P,则O,B分别为PF,PE的中点,△PEC也是等边三角形.
取EC的中点M,连结FM,MP,则FM⊥CE,MP⊥CE,
∴∠FMP为二面角F﹣CE﹣B的平面角.
在△MFP中,FM=MP= ![]() ,FP=2
,FP=2 ![]() ,
,
故cos∠FMP= ![]() =
= ![]() =-
=- ![]() ,
,
即二面角F﹣CE﹣B的余弦值为﹣ ![]()
【解析】(Ⅰ)连结OC,则OC⊥AB,从而得到OC⊥OE,进而得到OF⊥OE,由此能证明OF⊥EC. (Ⅱ)由(I)得AB=2AF.设AF=1,AB=2.由∠FCA为直线FC与平面ABC所成的角,知∠FCA=30°,由已知条件推导出∠FMP为二面角F﹣CE﹣B的平面角,由此能求出二面角F﹣CE﹣B的余弦值
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=3x2﹣2x,数列{an}的前n项和为Sn , 点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< ![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游公司为甲,乙两个旅游团提供四条不同的旅游线路,每个旅游团可任选其中一条旅游线路.
(1)求甲、乙两个旅游团所选旅游线路不同的概率;
(2)某天上午9时至10时,甲,乙两个旅游团都到同一个著名景点游览,20分钟后游览结束即离去.求两个旅游团在该著名景点相遇的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),满足f(x﹣2)=﹣f(x),且当x∈[0,1]时,f(x)=x2+x+sinx,若方程f(x)=m(m>0)在区间[﹣4,4]上有四个不同的根x1 , x2 , x3 , x4 , 则x1+x2+x3+x4的值为( )
A.2
B.﹣2
C.4
D.﹣4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上的一点A(2,4).
(Ⅰ)是否存在直线l:y=kx+3与圆M有两个交点B,C,并且|AB|=|AC|,若有,求此直线方程,若没有,请说明理由;
(Ⅱ)设点T(t,0)满足:存在圆M上的两点P和Q,使得 ![]() =
= ![]() ,求实数t的取值范围.
,求实数t的取值范围.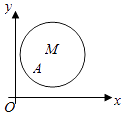
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣2
(Ⅰ)用定义法证明:函数f(x)在区间(﹣∞,1]上是减函数;
(Ⅱ)若函数g(x)=f(x)﹣mx是偶函数,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对应的边分别为a,b,c,且满足asinB= ![]() bcosA.
bcosA.
(1)求A的大小;
(2)若a=7,b=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为 ![]() .
.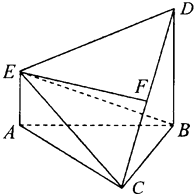
(1)若F是线段CD的中点,证明:EF⊥面DBC;
(2)求二面角D﹣EC﹣B的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com