练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    .如图，正方体ABCD-的棱长为2，动点E、F在棱上，动点P，Q分别在棱AD，CD上，若EF=1，E=x，DQ=y，DＰ＝ｚ（ｘ，ｙ，ｚ大于零），则四面体PEＦＱ的体积　(   ).　　　　　　　　　
    　　　　　　　　　　　　　　
    A．与ｘ，ｙ，ｚ都有关B．与ｘ有关，与ｙ，ｚ无关
    C．与ｚ有关，与ｘ，ｙ无关D．与ｙ有关，与ｘ，ｚ无关
    C

    四面体PEFQ的体积，找出三角形△EFQ面积是不变量，P到平面的距离是变化的，从而确定选项．
    解：从图中可以分析出，△EFQ的面积永远不变，为面A1B1CD面积的1/4
    而当P点变化时，它到面A1B1CD的距离是变化的，因此会导致四面体体积的变化．
    故选C
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计资料：
    x
    		2
    		3
    		4
    		5
    		6
    y
    		2.2
    		3.8
    		5.5
    		6.5
    		7.0
    若由资料可知y对x呈线性相关关系。试求：
    （1）线性回归方程；        
    （2）估计使用年限为10年时，维修费用是多少？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在一次实验中，采集到如下一组数据：

    		-2.0
    		-1.0
    		0
    		1.00
    		2.00
    		3.00

    		0.24
    		0.51
    		1
    		2.02
    		3.98
    		8.02
    则的函数关系与下列（  ）类函数最接近（其中为待定系数）
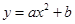    A．  B .   C.    D. 

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列两个变量之间的关系是相关关系的是（     ）
    A．角度和它的余弦值B．正方形的边长与它的面积
    C．电压一定时，电流与电阻D．日照时间与水稻的亩产量

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    为了分析某个高三学生的学习状态，对其下一阶段的学习作出预测和提供指导性建议，现对他前7次考试的数学成绩x、物理成绩y进行分析．下面是该生7次考试的成绩．
    数学
    		88
    		83
    		117
    		92
    		108
    		100
    		112
    物理
    		94
    		91
    		108
    		96
    		104
    		101
    		106
    （1)分别求出这个考生的他的数学平均成绩与物理平均成绩，并判断在这个学科中哪科成绩更稳定；
    （2)已知该生的物理成绩y与数学成绩x是线性相关的，求出线性回归方程；
    （3）若该生的物理成绩达到115分，请你估计他的数学成绩大约是多少？
    参考公式：，

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知某车间加工零件的个数与所花费时间之间的线性回归方程为,
    则加工600个零件大约需要的时间为
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知变量具有线性相关关系，且一组数据为，则回归方程为：
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若一函数模型为，将转化为的线性回归方程，需做变换＝
    A．B．C．D．以上都不对

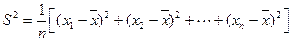
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    给出下列结论：
    （1）在回归分析中，可用相关指数R2的值判断模型的拟合效果，R2越大，模型的拟合效果越好；
    （2）在回归分析中，可用残差平方和判断模型的拟合效果，残差平方和越大，模型的拟合效果越好；
    （3）在回归分析中，可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适，带状区域的宽度越窄，说明模型的拟合精度越高。
    其中结论正确的是         。（把所有正确结论的序号填上）

    查看答案和解析>>

    同步练习册答案