已知O为A,B,C三点所在直线外一点,且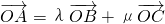 .数列{an},{bn}满足a1=2,b1=1,且
.数列{an},{bn}满足a1=2,b1=1,且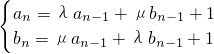 (n≥2).
(n≥2).
(Ⅰ)求λ+μ;
(Ⅱ)令cn=an+bn,求数列{cn}的通项公式;
(III)当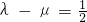 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.
解:(I)A,B,C三点共线,设
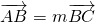
,
则

,(2分)
化简得:
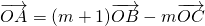
,所以λ=m+1,μ=-m,
所以λ+μ=1.(4分)
(II)由题设得
a
n+b
n=(λ+μ)(a
n-1+b
n-1)+2=a
n-1+b
n-1+2,(n≥2)(6分)
即c
n=c
n-1+2(n≥2),∴{c
n}是首项为a
1+b
1=3,
公差为2的等差数列,通项公式为c
n=2n+1(18分)
(III)由题设得
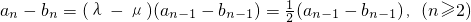
,(10分)
令d
n=a
n-b
n,则
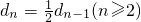
.
所以{d
n}是首项为a
1-b
1=1,公比为

的等比数列,
通项公式为
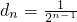
.(12分)
由
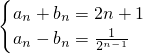
解得
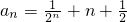
.(14分)
分析:(I)首先由A,B,C三点共线,可设
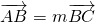
,
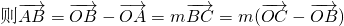
,经化简得
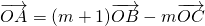
,即可知λ=m+1,μ=-m,进而得λ+μ=1
(II)首先根据已知及λ+μ=1可求出a
n+b
n=(λ+μ)(a
n-1+b
n-1)+2=a
n-1+b
n-1+2,(n≥2),则c
n=c
n-1+2(n≥2),即可求得数列{c
n}的通项公式为c
n=2n+1.
(III)首先由已知条件知要想求出a
n,得先求出
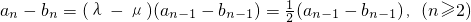
,再设令d
n=a
n-b
n,则
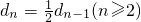
,即可求出{d
n}是首项为a
1-b
1=1,公比为

的等比数列,则通项公式为
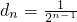
,由方程组
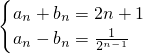
,进而可求出
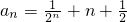
.
点评:本题主要利用三点共线的性质、数列的推导方法及数列的叠加进行相关的运算.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
已知O为A,B,C三点所在直线外一点,且
=λ+μ.数列{a
n},{b
n}满足a
1=2,b
1=1,且
| | an=λan-1+μbn-1+1 | | bn=μan-1+λbn-1+1 |
| |
(n≥2).
(Ⅰ)求λ+μ;
(Ⅱ)令c
n=a
n+b
n,求数列{c
n}的通项公式;
(III)当
λ-μ=时,求数列{a
n}的通项公式.
查看答案和解析>>
科目:高中数学
来源:中山区模拟
题型:解答题
已知O为A,B,C三点所在直线外一点,且
=λ+μ.数列{a
n},{b
n}满足a
1=2,b
1=1,且
| | an=λan-1+μbn-1+1 | | bn=μan-1+λbn-1+1 |
| |
(n≥2).
(Ⅰ)求λ+μ;
(Ⅱ)令c
n=a
n+b
n,求数列{c
n}的通项公式;
(III)当
λ-μ=时,求数列{a
n}的通项公式.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年广东省江门市鹤山一中高三(上)期中数学试卷(文科)(解析版)
题型:解答题
已知O为A,B,C三点所在直线外一点,且
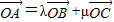
.数列{a
n},{b
n}满足a
1=2,b
1=1,且
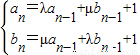
(n≥2).
(Ⅰ)求λ+μ;
(Ⅱ)令c
n=a
n+b
n,求数列{c
n}的通项公式;
(III)当
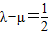
时,求数列{a
n}的通项公式.
查看答案和解析>>
科目:高中数学
来源:2009-2010学年广东省中山市高三诊断数学试卷(理科)(解析版)
题型:解答题
已知O为A,B,C三点所在直线外一点,且
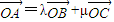
.数列{a
n},{b
n}满足a
1=2,b
1=1,且
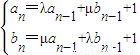
(n≥2).
(Ⅰ)求λ+μ;
(Ⅱ)令c
n=a
n+b
n,求数列{c
n}的通项公式;
(III)当
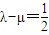
时,求数列{a
n}的通项公式.
查看答案和解析>>
科目:高中数学
来源:2009年广东省佛山市高考数学一模试卷(文科)(解析版)
题型:解答题
已知O为A,B,C三点所在直线外一点,且
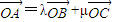
.数列{a
n},{b
n}满足a
1=2,b
1=1,且
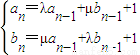
(n≥2).
(Ⅰ)求λ+μ;
(Ⅱ)令c
n=a
n+b
n,求数列{c
n}的通项公式;
(III)当
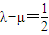
时,求数列{a
n}的通项公式.
查看答案和解析>>

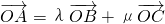 .数列{an},{bn}满足a1=2,b1=1,且
.数列{an},{bn}满足a1=2,b1=1,且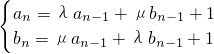 (n≥2).
(n≥2).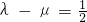 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.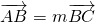 ,
, ,(2分)
,(2分)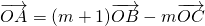 ,所以λ=m+1,μ=-m,
,所以λ=m+1,μ=-m,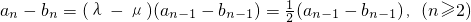 ,(10分)
,(10分)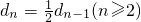 .
. 的等比数列,
的等比数列,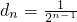 .(12分)
.(12分)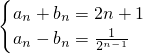
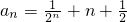 .(14分)
.(14分)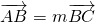 ,
,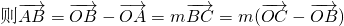 ,经化简得
,经化简得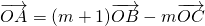 ,即可知λ=m+1,μ=-m,进而得λ+μ=1
,即可知λ=m+1,μ=-m,进而得λ+μ=1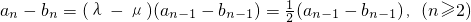 ,再设令dn=an-bn,则
,再设令dn=an-bn,则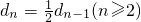 ,即可求出{dn}是首项为a1-b1=1,公比为
,即可求出{dn}是首项为a1-b1=1,公比为 的等比数列,则通项公式为
的等比数列,则通项公式为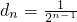 ,由方程组
,由方程组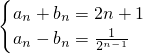 ,进而可求出
,进而可求出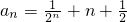 .
.

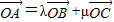 .数列{an},{bn}满足a1=2,b1=1,且
.数列{an},{bn}满足a1=2,b1=1,且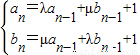 (n≥2).
(n≥2).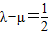 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.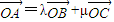 .数列{an},{bn}满足a1=2,b1=1,且
.数列{an},{bn}满足a1=2,b1=1,且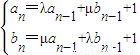 (n≥2).
(n≥2).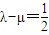 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.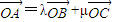 .数列{an},{bn}满足a1=2,b1=1,且
.数列{an},{bn}满足a1=2,b1=1,且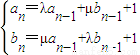 (n≥2).
(n≥2).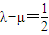 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.