
【题目】如图,已知 ![]() =(2,1),
=(2,1), ![]() =(1,7),
=(1,7), ![]() =(5,1),设Z是直线OP上的一动点.
=(5,1),设Z是直线OP上的一动点. 
(1)求使 ![]()
![]() 取最小值时的
取最小值时的 ![]() ;
;
(2)对(1)中求出的点Z,求cos∠AZB的值.
【答案】
(1)∵Z是直线OP上的一点,
∴ ![]() ∥
∥ ![]() ,
,
设实数t,使 ![]() =t
=t ![]() ,
,
∴ ![]() =t(2,1)=(2t,t),
=t(2,1)=(2t,t),
则 ![]() =
= ![]() ﹣
﹣ ![]() =(1,7)﹣(2t,t)=(1﹣2t,7﹣t),
=(1,7)﹣(2t,t)=(1﹣2t,7﹣t),
![]() =
= ![]() ﹣
﹣ ![]() =(5,1)﹣(2t,t)=(5﹣2t,1﹣t).
=(5,1)﹣(2t,t)=(5﹣2t,1﹣t).
∴ ![]()
![]() =(1﹣2t)(5﹣2t)+(7﹣t)(1﹣t)
=(1﹣2t)(5﹣2t)+(7﹣t)(1﹣t)
=5t2﹣20t+12=5(t﹣2)2﹣8.
当t=2时, ![]()
![]() 有最小值﹣8,
有最小值﹣8,
此时 ![]() =(2t,t)=(4,2)
=(2t,t)=(4,2)
(2)当t=2时, ![]() =(1﹣2t,7﹣t)=(﹣3,5),|
=(1﹣2t,7﹣t)=(﹣3,5),| ![]() |=
|= ![]() ,
,
![]() =(5﹣2t,1﹣t)=(1,﹣1),|
=(5﹣2t,1﹣t)=(1,﹣1),| ![]() |=
|= ![]() .
.
故cos∠AZB═ 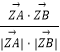 =
= ![]()
=﹣ ![]() =﹣
=﹣
【解析】(1)运用向量共线的坐标表示,求得向量ZA,ZB的坐标,由数量积的标准表示,结合二次函数的最值求法,可得最小值,及向量OZ;(2)求得t=2的向量ZA,ZB,以及模的大小,由向量的夹角公式,计算即可得到.


科目:高中数学 来源: 题型:
【题目】为研究心理健康与是否是留守儿童的关系,某小学在本校四年级学生中抽取了一个110人的样本,其中留守儿童有40人,非留守儿童有70人,对他们进行了心理测试,并绘制了如图的等高条形图,试问:能否在犯错误的概率不超过0.001的前提下认为心理健康与是否是留守儿童有关系?
参考数据:
P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() (n=a+b+c+d)
(n=a+b+c+d)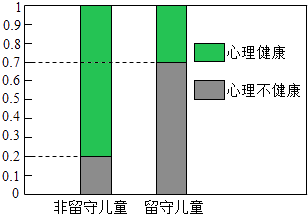
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种出口产品的关税税率t.市场价格x(单位:千元)与市场供应量p(单位:万件)之间近似满足关系式:![]() ,其中k.b均为常数.当关税税率为75%时,若市场价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件.
,其中k.b均为常数.当关税税率为75%时,若市场价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件.
(1)试确定k.b的值;
(2)市场需求量q(单位:万件)与市场价格x近似满足关系式:![]() .P = q时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率
.P = q时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一解三角形的题目因纸张破损,有一条件不清,具体如下:在△ABC中,已知a= ![]() ,2cos2
,2cos2 ![]() =(
=( ![]() ﹣1)cosB,c= , 求角A,若该题的答案是A=60°,请将条件补充完整.
﹣1)cosB,c= , 求角A,若该题的答案是A=60°,请将条件补充完整.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(n)是定义在N*上的增函数,f(4)=5,且满足:
①任意n∈N*,f(n)![]() Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:f′(x)>1﹣f(x),f(0)=3,f′(x)是f(x)的导函数,则不等式exf(x)>ex+2(其中e为自然对数的底数)的解集为( )
A.{x|x>0}
B.{x|x<0}
C.{x|x<﹣1或x>1}
D.{x|x<﹣1或0<x<1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心(a,b)(a<0,b<0)在直线y=2x+1上的圆,若其圆心到x轴的距离恰好等于圆的半径,在y轴上截得的弦长为 ![]() ,则圆的方程为( )
,则圆的方程为( )
A.(x+2)2+(y+3)2=9
B.(x+3)2+(y+5)2=25
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1,2,3,4,5的卡片,这5张卡片除号码外完全相同,现进行有放回的连续抽取两次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求条件“取出卡片的号码之和不小于7或小于5”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f′(x)是二次函数,如图是f′(x)的大致图象,若f(x)的极大值与极小值的和等于 ![]() ,则f(0)的值为( )
,则f(0)的值为( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com