
【题目】已知关于x的不等式![]() 的解集为
的解集为![]() .
.
(1)求a,b的值.
(2)当![]() 时,解关于x的不等式
时,解关于x的不等式![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
试题
(1)利用韦达定理可得![]() ;
;
(2)结合(1)的结论分类讨论实数c的范围即可求得不等式的解集.
试题解析:
解:(1)因为不等式ax2-3x+2>0的解集为{x|x<1或x>b}
所以x1=1与x2=b是方程ax2-3x+2=0的两个实数根
b>1且a>0
得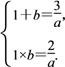 解得
解得![]()
(2)不等式ax2-(ac+b)x+bc<0,
即x2-(2+c)x+2c<0,即(x-2)(x-c)<0.
当c>2时,不等式(x-2)(x-c)<0的解集为{x|2<x<c};
当c<2时,不等式(x-2)(x-c)<0的解集为{x|c<x<2};
当c=2时,不等式(x-2)(x-c)<0的解集为


科目:高中数学 来源: 题型:
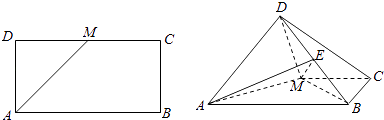
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
(Ⅱ)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的虚轴长为
的虚轴长为![]() ,两条渐近线方程为
,两条渐近线方程为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)双曲线![]() 上有两个点
上有两个点![]() ,直线
,直线![]() 和
和![]() 的斜率之积为
的斜率之积为![]() ,判别
,判别![]() 是否为定值,;
是否为定值,;
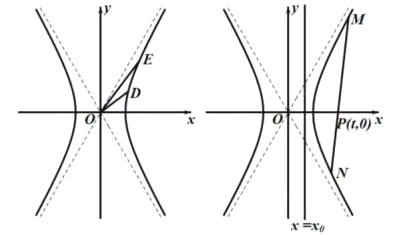
(3)经过点![]() 的直线
的直线![]() 且与双曲线
且与双曲线![]() 有两个交点
有两个交点![]() ,直线
,直线![]() 的倾斜角是
的倾斜角是![]() ,是否存在直线
,是否存在直线![]() (其中
(其中![]() )使得
)使得![]() 恒成立?(其中
恒成立?(其中![]() 分别是点
分别是点![]() 到
到![]() 的距离)若存在,求出
的距离)若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可参加一次抽奖.随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商场对前5天抽奖活动的人数进行统计,y表示第x天参加抽奖活动的人数,得到统计表如下:
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析,发现y与x具有线性相关关系.
(1)若从这5天随机抽取两天,求至少有1天参加抽奖人数超过70的概率;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ,并估计该活动持续7天,共有多少名顾客参加抽奖?
,并估计该活动持续7天,共有多少名顾客参加抽奖?
参考公式及数据: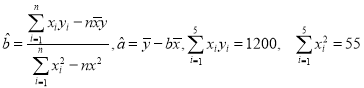 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50人测量身高.据测量,被测学生身高全部介于![]() 到
到![]() 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组![]() ;第二组
;第二组![]() ;…;第八组
;…;第八组![]() .如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
.如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.

(1)估计这所学校高三年级全体男生身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为![]() ,求满足“
,求满足“![]() ”的事件的概率.
”的事件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和是Sn , 且Sn+ ![]() an=1,数列{bn},{cn}满足bn=log3
an=1,数列{bn},{cn}满足bn=log3 ![]() ,cn=
,cn= ![]() . (Ⅰ)求数列{an}的通项公式;
. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列{cn}的前n项和为Tn , 若不等式Tn<m对任意的正整数n恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD. (Ⅰ)求证:AD⊥平面BFED;
(Ⅱ)在线段EF上是否存在一点P,使得平面PAB与平面ADE所成的锐二面角的余弦值为 ![]() .若存在,求出点P的位置;若不存在,说明理由.
.若存在,求出点P的位置;若不存在,说明理由.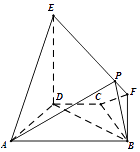
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com