
| A. | (-∞,0] | B. | [-2,2] | C. | (-∞,2] | D. | [0,2] |
分析 由f(x)的解析式可得当x≤0时,2x-1≥-1,结合指数函数的值域即可判断;再由x>0时,x2-ax≥-1,结合参数分离和基本不等式即可得到a的范围.
解答 解:由f(x)≥-1在R上恒成立,可得
当x≤0时,2x-1≥-1,即2x≥0显然成立;
又x>0时,x2-ax≥-1,即为a≤$\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$,
由x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,
当且仅当x=1时取得最小值2,可得a≤2.
综上可得a≤2.
故选:C.
点评 本题考查函数恒成立问题的解法,注意运用指数函数的值域和二次不等式的恒成立问题的解法,运用参数分离和基本不等式,考查化简整理的运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2.
如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1-BCDE.(Ⅰ) 证明:CD⊥平面A1OC;
如图1,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1-BCDE.(Ⅰ) 证明:CD⊥平面A1OC;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
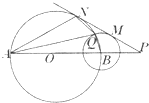 如图,以AB为直径的圆O与以N为圆心,半径为1的圆一个交点为Q,延长AB至点P,过点P作两圆的切线,分别切于M,N两点,已知AB=4.
如图,以AB为直径的圆O与以N为圆心,半径为1的圆一个交点为Q,延长AB至点P,过点P作两圆的切线,分别切于M,N两点,已知AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com