
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)若![]() ,试讨论函数
,试讨论函数![]() 的零点个数.
的零点个数.
科目:高中数学 来源: 题型:
【题目】山东省2020年高考将实施新的高考改革方案.考生的高考总成绩将由3门统一高考科目成绩和自主选择的3门普通高中学业水平等级考试科目成绩组成,总分为750分.其中,统一高考科目为语文、数学、外语,自主选择的3门普通高中学业水平等级考试科目是从物理、化学、生物、历史、政治、地理6科中选择3门作为选考科目,语、数、外三科各占150分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.根据高考综合改革方案,将每门等级考试科目中考生的原始成绩从高到低分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共8个等级。参照正态分布原则,确定各等级人数所占比例分别为
共8个等级。参照正态分布原则,确定各等级人数所占比例分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .等级考试科目成绩计入考生总成绩时,将
.等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则,分别转换到91-100、81-90、71-80,61-70、51-60、41-50、31-40、21-30八个分数区间,得到考生的等级成绩.
等级内的考生原始成绩,依照等比例转换法则,分别转换到91-100、81-90、71-80,61-70、51-60、41-50、31-40、21-30八个分数区间,得到考生的等级成绩.
举例说明.
某同学化学学科原始分为65分,该学科![]() 等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属
等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属![]() 等级.而
等级.而![]() 等级的转换分区间为61~70,那么该同学化学学科的转换分为:
等级的转换分区间为61~70,那么该同学化学学科的转换分为:
设该同学化学科的转换等级分为![]() ,
,![]() ,求得
,求得![]() .
.
四舍五入后该同学化学学科赋分成绩为67.
(1)某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布![]() .
.
(i)若小明同学在这次考试中物理原始分为84分,等级为![]() ,其所在原始分分布区间为82~93,求小明转换后的物理成绩;
,其所在原始分分布区间为82~93,求小明转换后的物理成绩;
(ii)求物理原始分在区间![]() 的人数;
的人数;
(2)按高考改革方案,若从全省考生中随机抽取4人,记![]() 表示这4人中等级成绩在区间
表示这4人中等级成绩在区间![]() 的人数,求
的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可应用到有限维空间,并构成一般不动点定理的基石.布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔(L.E. J. Brouwer),简单的讲就是对于满足一定条件的连续函数![]() ,存在一个点
,存在一个点![]() ,使得
,使得![]() ,那么我们称该函数为“不动点”函数,下列为“不动点”函数的是( )
,那么我们称该函数为“不动点”函数,下列为“不动点”函数的是( )
A.![]() B.
B.![]()
C.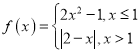 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为发挥体育咋核心素养时代的独特育人价值,越来越多的中学生已将某些体育项目纳入到学生的必修课程,某中学计划在高一年级开设游泳课程,为了解学生对游泳的兴趣,某数学研究学习小组随机从该校高一年级学生抽取了100人进行调查.
班 级 | 一(1) | 一(2) | 一(3) | 一(4) | 一(5) | 一(6) | 一(7) | 一(8) | 一(9) | 一(10) |
市级比赛 获奖人数 | 2 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 2 |
市级以上比 赛获奖人数 | 2 | 2 | 1 | 0 | 2 | 3 | 3 | 2 | 1 | 2 |
(1)已知在被抽取的女生中有6名高一(1)班学生,其中3名对游泳有兴趣,现在从这6名学生中最忌抽取3人,求至少有2人对游泳有兴趣的概率;
(2)该研究性学习小组在调查发现,对游泳有兴趣的学生中有部分曾在市级以上游泳比赛中获奖,如上表所示,若从高一(8)班和高一(9)班获奖学生中随机各抽取2人进行跟踪调查.记选中的4人中市级以上游泳比赛获奖的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
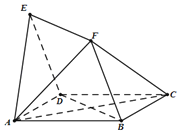
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,且与直线
,且与直线![]() 相切,椭圆
相切,椭圆![]() 的对称轴为坐标轴,
的对称轴为坐标轴,![]() 点为坐标原点,
点为坐标原点,![]() 是其一个焦点,又点
是其一个焦点,又点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的标准方程和椭圆
的标准方程和椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 的动直线
的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 点,交轨迹
点,交轨迹![]() 于
于![]() 两点,设
两点,设![]() 为
为![]() 的面积,
的面积,![]() 为
为![]() 的面积,令
的面积,令![]() 的面积,令
的面积,令![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com