
【题目】设![]() ,函数
,函数![]() ,
,![]() 为函数
为函数![]() 的导函数.
的导函数.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 与函数
与函数![]() 存在相同的零点,求实数a的值;
存在相同的零点,求实数a的值;
(3)求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(1)见解析(2)![]() (3)
(3)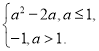
【解析】
(1)首先求出函数的导函数![]() ,再对
,再对![]() 分类讨论可得;
分类讨论可得;
(2)由(1)可知![]() 时,函数
时,函数![]() 的零点是
的零点是![]() ,经检验不符题意,当
,经检验不符题意,当![]() 时,函数
时,函数![]() 的零点是
的零点是![]() 和
和![]() ,分别计算可得;
,分别计算可得;
(3)结合(1)求出![]() ,再分类讨论可得.
,再分类讨论可得.
解:(1)因为![]()
所以![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,当
时,当![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 和在
和在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
同理当![]() 时,函数
时,函数![]() 在
在![]() 和在
和在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)当![]() 时,函数
时,函数![]() 的零点是0,而
的零点是0,而![]() ,所以不合题意,舍去;
,所以不合题意,舍去;
当![]() 时,函数
时,函数![]() 的零点是
的零点是![]() 和
和![]() ,
,
因为![]() ,
,
所以由函数![]() 与函数
与函数![]() 存在相同的零点,
存在相同的零点,
得![]() ,即
,即![]() ,解得
,解得![]() .
.
(3)由(1)得,
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,此时函数
上单调递增,此时函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ;
;
当![]() ,即
,即![]() 时,
时,
函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ;
;
当![]() ,即
,即![]() 时,
时,
因为![]() ,
,![]() ,
,
所以![]() ,此时函数的最小值为
,此时函数的最小值为![]() .
.
所以函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为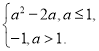


科目:高中数学 来源: 题型:
【题目】自2016年1月1日全面实施二孩政策以来,为了了解生二孩意愿与年龄段是否有关,某市选取“75后”和“80后”两个年龄段的已婚妇女作为调查对象,进行了问卷调查,共调查了40名“80后”,40名“75后”,其中调查的“80后”有10名不愿意生二孩,其余的全部愿意生二孩;调查的“75后”有5人不愿意生二孩,其余的全部愿意生二孩.
(1)根据以上数据完成下列![]() 列联表;
列联表;
年龄段 | 不愿意 | 愿意 | 合计 |
“80后” | |||
“75后” | |||
合计 |
(2)根据![]() 列联表,能否在犯错误的概率不超过0.05的前提下,认为“生二孩意愿与年龄段有关”?请说明理由.
列联表,能否在犯错误的概率不超过0.05的前提下,认为“生二孩意愿与年龄段有关”?请说明理由.
参考公式: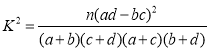 (其中
(其中![]() )
)
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P-ABC(如图一)的平面展开图(如图二)中,四边形ABCD为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥P-ABC中:
均为正三角形,在三棱锥P-ABC中:
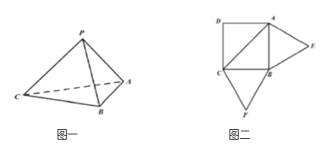
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上运动,当直线BM与平面PAC所成的角最大时,求直线MA与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 的导函数
的导函数![]() 是奇函数(
是奇函数(![]() ),则称函数
),则称函数![]() 是“双奇函数” .函数
是“双奇函数” .函数![]() .
.
(1)若函数![]() 是“双奇函数”,求实数
是“双奇函数”,求实数![]() 的值;
的值;
(2)假设![]() .
.
(i)在(1)的条件下,讨论函数![]() 的单调性;
的单调性;
(ii)若![]() ,讨论函数
,讨论函数![]() 的极值点.
的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学参加化学竞赛初赛,考试分为笔试、口试、实验三个项目,各单项通过考试的概率依次为![]() 、
、![]() 、
、![]() ,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
(Ⅰ)若规定总分不低于8分即可进入复赛,求甲同学进入复赛的概率;
(Ⅱ)记三个项目中通过考试的个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() 交于点
交于点![]() ,
,![]() 是
是![]() 上任意一点.
上任意一点.
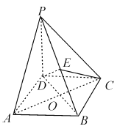
(1)求证![]() ;
;
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com