
【题目】已知直线l的方程为3x+4y-12=0,求直线l′的方程,使得:
(1)l′与l平行且过点(-1,3);
(2)l′与l垂直且l′与两坐标轴围成的三角形的面积为4.
【答案】(1) 3x+4y-9=0. (2) 4x-3y+4![]() =0或4x-3y-4
=0或4x-3y-4![]() =0.
=0.
【解析】
(1)根据直线的平行关系可设![]() 的方程为
的方程为![]() ,将点
,将点![]() 代入求出
代入求出![]() 的值即可;(2)根据直线的垂直关系可将直线
的值即可;(2)根据直线的垂直关系可将直线![]() 设为
设为![]() ,分别求出其在坐标轴上的截距,结合三角形面积公式求出
,分别求出其在坐标轴上的截距,结合三角形面积公式求出![]() 即可.
即可.
(1)设l′的方程为3x+4y+m=0,
由点(-1,3)在l′上知,-3+12+m=0m=-9,
所以直线l′的方程为3x+4y-9=0.
(2)设l′的方程为4x-3y+λ=0,
令y=0,得x=-![]() ,令x=0,得y=
,令x=0,得y=![]() ,
,
于是三角形面积S=![]() |-
|-![]() |·|
|·|![]() |=4,
|=4,
得λ2=96λ=±4![]() ,
,
所以直线l′的方程为4x-3y+4![]() =0或4x-3y-4
=0或4x-3y-4![]() =0.
=0.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】已知p:x2-(3+a)x+3a<0,其中a<3;q:x2+4x-5>0.
(1)若p是q的必要不充分条件,求实数a的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
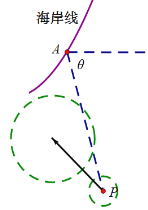
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市A(看做一点)的东偏南![]() 角方向
角方向![]() ,300 km的海面P处,并以20km / h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10km / h的速度不断增大.
,300 km的海面P处,并以20km / h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10km / h的速度不断增大.
(1) 问10小时后,该台风是否开始侵袭城市A,并说明理由;
(2) 城市A受到该台风侵袭的持续时间为多久?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设10张奖券中有一等奖奖券1张,可获价值50元的奖品,有二等奖奖券3张,每张可获价值10元的奖品,其余6张没有奖品.
(1)顾客甲从10张奖券中任意抽取1张,求中奖次数X的概率分布;
(2)顾客乙从10张奖券中任意抽取2张,
①求顾客乙中奖的概率;
②设顾客乙获得的奖品总价值Y元,求Y的概率分布及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下考古活动中,需要潜水员潜入水深为30米的水底进行作业.其用氧量包含3个方面:①下潜时,平均速度为![]() (米/单位时间),单位时间内用氧量为
(米/单位时间),单位时间内用氧量为![]() (
(![]() 为正常数);②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为
为正常数);②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为![]() (米/单位时间), 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为
(米/单位时间), 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为![]() .
.
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)设0<![]() ≤5,试确定下潜速度
≤5,试确定下潜速度![]() ,使总的用氧量最少.
,使总的用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品8件和B类产品15件,乙种设备每天能生产A类产品10件和B类产品25件,已知设备甲每天的租赁费300元,设备乙每天的租赁费400元,现车间至少要生产A类产品100件,B类产品200件,所需租赁费最少为__元![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com