
【题目】如图,在半径为![]() ,圆心角为
,圆心角为![]() 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形![]() ,并且
,并且![]() 与
与![]() 的平分线
的平分线![]() 平行,设
平行,设![]() .
.

(1)试将长方形![]() 的面积
的面积![]() 表示为
表示为![]() 的函数;
的函数;
(2)若将长方形![]() 弯曲,使
弯曲,使![]() 和
和![]() 重合焊接制成圆柱的侧面,当圆柱侧面积最大时,求圆柱的体积(假设圆柱有上下底面);为了节省材料,想从△
重合焊接制成圆柱的侧面,当圆柱侧面积最大时,求圆柱的体积(假设圆柱有上下底面);为了节省材料,想从△![]() 中直接剪出一个圆面作为圆柱的一个底面,请问是否可行?并说明理由.
中直接剪出一个圆面作为圆柱的一个底面,请问是否可行?并说明理由.
(参考公式:圆柱体积公式![]() .其中
.其中![]() 是圆柱底面面积,
是圆柱底面面积,![]() 是圆柱的高;等边三角形内切圆半径
是圆柱的高;等边三角形内切圆半径![]() .其中
.其中![]() 是边长)
是边长)
科目:高中数学 来源: 题型:
【题目】设函数![]() ,则下列命题中正确的个数是( )
,则下列命题中正确的个数是( )
①当![]() 时,函数
时,函数![]() 在
在![]() 上是单调增函数;
上是单调增函数;
②当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值;
上有最小值;
③函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
④方程![]() 可能有三个实数根.
可能有三个实数根.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,
平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() 平面BCE;
平面BCE;
(2)求证:![]() 平面BCE;
平面BCE;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校早上8:00开始上课,假设该校学生小张与小王在早上7:30~7:50之间到校,且每人在该时间段的任何时刻到校是等可能的,则小张比小王至少晚5分钟到校的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知关于![]() 的一次函数
的一次函数![]()
(1)设集合![]() 和
和![]() 分别从集合
分别从集合![]() 和
和![]() 中随机取一个数作为
中随机取一个数作为![]() 和
和![]() ,求函数
,求函数![]() 是增函数的概率;
是增函数的概率;
(2)实数![]() 满足条件
满足条件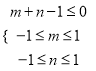 求函数
求函数![]() 的图象经过一、二、三象限的概率.
的图象经过一、二、三象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是( )
A.奇函数,且在(0,1)上是增函数
B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数
D.偶函数,且在(0,1)上是减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com