
【题目】甲、乙两人各射击一次,击中目标的概率分别是![]() 和
和![]() ,假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
,假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(1)求甲射击4次,至多1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击,求乙恰好射击5次后被中止射击的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由题意知,甲击中目标的概率为![]() ,未击中目标的概率为
,未击中目标的概率为![]() ,甲射击4次,相当于4次独立重复试验,根据独立重复试验的概率公式,即可求出至多1次未击中目标的概率;
,甲射击4次,相当于4次独立重复试验,根据独立重复试验的概率公式,即可求出至多1次未击中目标的概率;
(2)两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次,表示相互独立的两个事件同时发生,写出两个事件的概率,根据相互独立事件的概率公式得到结果;
(3)乙恰好射击5次后,被中止射击,表示乙必须在第4、第5次没有射中,第3次射中,在第1、第2次射击中至少射中一次,根据相互独立事件同时发生的概率得到结果.
(1)由题可知,每次射击是否击中目标,相互之间没有影响,
甲击中目标的概率为![]() ,未击中目标的概率为
,未击中目标的概率为![]() ,
,
甲射击4次,相当于4次独立重复试验,
设“至多1次未击中目标”为事件![]() ,
,
则概率为:![]() .
.
(2)根据题意,乙击中目标的概率为![]() ,未击中目标的概率为
,未击中目标的概率为![]() ,
,
记“甲射击4次,恰好击中目标2次”为事件![]() ,
,
“乙射击4次,恰好击中目标3次”为事件![]() ,
,
![]() ,
,
![]() ,
,
由于甲、乙射击相互独立,
故![]() ,
,
即两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率为![]() .
.
(3)根据题意,可知连续2次未击中目标,则停止射击,
记“乙恰好射击5次后,被中止射击”为事件![]() ,
,
由于乙恰好射击5次后被中止射击,
则乙必须在第4、第5次没有射中,第3次射中,在第1、第2次射击中至少射中一次,
所以概率为: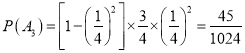 .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)2﹣alnx(a<0).
(1)讨论f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2(x1<x2),且关于x的方程f(x)=b(b∈R)恰有三个实数根x3,x4,x5(x3<x4<x5),求证:2(x2﹣x1)>x5﹣x3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意实数![]() 给出下列命题:①“
给出下列命题:①“![]() ”是“
”是“![]() ”的充要条件;②“
”的充要条件;②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;③“
是无理数”的充要条件;③“![]() ”是“
”是“![]() ”的充分条件;④“
”的充分条件;④“![]() ”是“
”是“![]() ”的必要条件.其中真命题的个数是( )
”的必要条件.其中真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查中学生平均每人每天参加体育锻炼的时间![]() (单位:
(单位:![]() ),按锻炼时间分下列四种情况统计:(1)
),按锻炼时间分下列四种情况统计:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() 以上,有10000名中学生参加了此项活动,下图是此次调查中某一项的流程图,若平均每天参加体育锻炼的时间在
以上,有10000名中学生参加了此项活动,下图是此次调查中某一项的流程图,若平均每天参加体育锻炼的时间在![]() 的学生频率是0.15,则输出的结果为________.
的学生频率是0.15,则输出的结果为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】衣橱中有5件上衣,其中2件蓝色、3件白色,有8条裤子,其中3条蓝色、5条黑色.则随机取一件上衣和一条裤子,上衣与裤子同色的概率为________,上衣和裤子中至少有一个为蓝色的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对旗下的甲、乙两个门店在1至9月份的营业额(单位:万元)进行统计并得到如图折线图.

下面关于两个门店营业额的分析中,错误的是( )
A.甲门店的营业额折线图具有较好的对称性,故而营业额的平均值约为32万元
B.根据甲门店的营业额折线图可知,该门店营业额的平均值在[20,25]内
C.根据乙门店的营业额折线图可知,其营业额总体是上升趋势
D.乙门店在这9个月份中的营业额的极差为25万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a,b,c,已知sinC+cosC=1-sin![]() .
.
(1)求sinC的值;
(2)若a2+b2=4(a+b)-8,求边c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两城市![]() 和
和![]() 相距
相距![]() ,现计划在两城市外以
,现计划在两城市外以![]() 为直径的半圆
为直径的半圆![]() 上选择一点
上选择一点![]() 建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城
建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城![]() 和城
和城![]() 的总影响度为城
的总影响度为城![]() 和城
和城![]() 的影响度之和,记
的影响度之和,记![]() 点到城
点到城![]() 的距离为
的距离为![]() ,建在
,建在![]() 处的垃圾处理场对城
处的垃圾处理场对城![]() 和城
和城![]() 的总影响度为
的总影响度为![]() ,统计调查表明:垃圾处理场对城
,统计调查表明:垃圾处理场对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为4,对城
的距离的平方成反比,比例系数为4,对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为
的距离的平方成反比,比例系数为![]() ,当垃圾处理场建在
,当垃圾处理场建在![]() 的中点时,对城
的中点时,对城![]() 和城
和城![]() 的总影响度为0.065;
的总影响度为0.065;
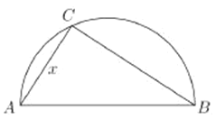
(1)将![]() 表示成
表示成![]() 的函数;
的函数;
(2)判断![]() 上是否存在一点,使建在此处的垃圾处理场对城
上是否存在一点,使建在此处的垃圾处理场对城![]() 和城
和城![]() 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城![]() 的距离;若不存在,说明理由;
的距离;若不存在,说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com