解:(1)由已知得:f(x)=2f(x+2)=4f(x+4),
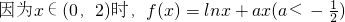
,设x∈(-4,-2)时,则x+4∈(0,2),
所以f(x+4)=ln(x+4)+a(x+4)
∴x∈(-4,-2)时,f(x)=4f(x+4)=4ln(x+4)+4a(x+4)
∴
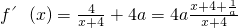
,∵
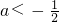
,∴

,
∴当
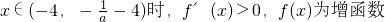
,
当
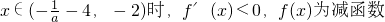
,
∴
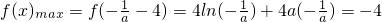
,∴a=-1
∴当x∈(0,2)时,f(x)=lnx-x
(2)由(1)可得:x∈(0,1)∪(1,2)时,不等式
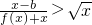
恒成立,
即为

恒成立,
①当x∈(0,1)时,

,令
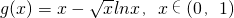
则
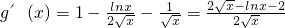
令
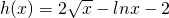
,则当x∈(0,1)时,
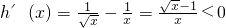
∴h(x)>h(1)=0,∴
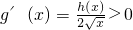
,
∴g(x)<g(1)=1,故此时只需b≥1即可;
②当x∈(1,2)时,
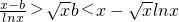
,令
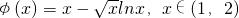
则
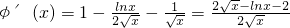
令
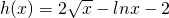
,则当x∈(1,2)时,

∴h(x)>h(1)=0,∴
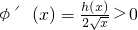
,
∴φ(x)<φ(1)=1,故此时只需b≤1即可,
综上所述:b=1,因此满足题中b的取值集合为:{1}
分析:(1)由已知得:f(x)=2f(x+2)=4f(x+4),设x∈(-4,-2)时,则x+4∈(0,2),代入
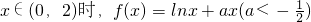
,求出f(x+4)=ln(x+4)+a(x+4),再根据当x∈(-4,-2)时,f(x)的最大值为-4,利用导数求得它的最大值,解方程即可求得a的值,进而求得结论;
(2)假设存在实数b使得不等式
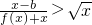
对于x∈(0,1)∪(1,2)时恒成立,由(1)可得:x∈(0,1)∪(1,2)时,不等式
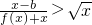
恒成立,利用分离参数的方法,转化为求函数的最值问题,即可求得b的值.
点评:此题是个难题.考查函数解析式的求法以及函数恒成立问题,体现了转化和分类讨论的思想方法,其中问题(2)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

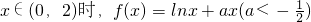 ,当x∈(-4,-2)时,f(x)的最大值为-4.
,当x∈(-4,-2)时,f(x)的最大值为-4.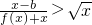 对于x∈(0,1)∪(1,2)时恒成立,若存在,求出实数 b的取值集合,若不存在,说明理由.
对于x∈(0,1)∪(1,2)时恒成立,若存在,求出实数 b的取值集合,若不存在,说明理由.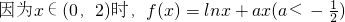 ,设x∈(-4,-2)时,则x+4∈(0,2),
,设x∈(-4,-2)时,则x+4∈(0,2),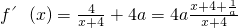 ,∵
,∵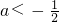 ,∴
,∴ ,
,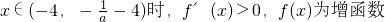 ,
,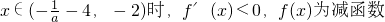 ,
,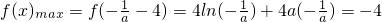 ,∴a=-1
,∴a=-1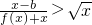 恒成立,
恒成立, 恒成立,
恒成立, ,令
,令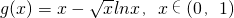
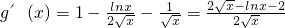
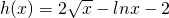 ,则当x∈(0,1)时,
,则当x∈(0,1)时,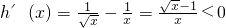
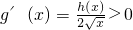 ,
,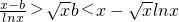 ,令
,令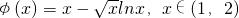
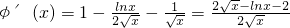
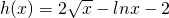 ,则当x∈(1,2)时,
,则当x∈(1,2)时,
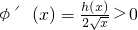 ,
,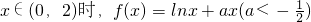 ,求出f(x+4)=ln(x+4)+a(x+4),再根据当x∈(-4,-2)时,f(x)的最大值为-4,利用导数求得它的最大值,解方程即可求得a的值,进而求得结论;
,求出f(x+4)=ln(x+4)+a(x+4),再根据当x∈(-4,-2)时,f(x)的最大值为-4,利用导数求得它的最大值,解方程即可求得a的值,进而求得结论;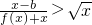 对于x∈(0,1)∪(1,2)时恒成立,由(1)可得:x∈(0,1)∪(1,2)时,不等式
对于x∈(0,1)∪(1,2)时恒成立,由(1)可得:x∈(0,1)∪(1,2)时,不等式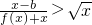 恒成立,利用分离参数的方法,转化为求函数的最值问题,即可求得b的值.
恒成立,利用分离参数的方法,转化为求函数的最值问题,即可求得b的值.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案