
【题目】定义区间(m,n),![]() ,
,![]() ,
,![]() 的长度均为
的长度均为![]() ,其中
,其中![]() .
.
(1)若关于x的不等式![]() 的解集构成的区间的长度为
的解集构成的区间的长度为![]() ,求实数a的值;
,求实数a的值;
(2)求关于x的不等式![]() 的解集构成的区间的长度的取值范围;
的解集构成的区间的长度的取值范围;
(3)已知关于x的不等式组 的解集构成的各区间长度和为5,求实数t的取值范围.
的解集构成的各区间长度和为5,求实数t的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)观察二次项的系数带有字母,需要先对字母进行讨论,当a等于0时,看出合不合题意,![]() 时,方程
时,方程![]() 的两根设为
的两根设为![]() ,根据根与系数之间的关系,写出两根的和与积,表示出区间长度,得到结果(2)根据所给的函数式,利用三角函九公式进行化简求值,根据二次不等式出不等式成立的条件,由此能求出结果(3)先解关于x的不等式组,解出两个不等式的解集,求两个不等式的解集的交集,
,根据根与系数之间的关系,写出两根的和与积,表示出区间长度,得到结果(2)根据所给的函数式,利用三角函九公式进行化简求值,根据二次不等式出不等式成立的条件,由此能求出结果(3)先解关于x的不等式组,解出两个不等式的解集,求两个不等式的解集的交集,![]() ,不等式组的解集的各区间长度和为6,写出不等式组进行讨论,得到结果.
,不等式组的解集的各区间长度和为6,写出不等式组进行讨论,得到结果.
(1)当![]() 时,不等式
时,不等式![]() 的解为
的解为![]() ,不成立;
,不成立;
当![]() 时,方程
时,方程![]() 的两根设为
的两根设为![]() ,则
,则![]() ,
,![]() ,
,
由题意知![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
所以![]() .
.
(2)![]() ,
,
![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() 的解集为
的解集为![]() ,
,
当![]() 时,
时,![]() 的解集为
的解集为![]() ,
,
∴关于x的不等式![]() 的解集构成的区间的长度的取值范围是
的解集构成的区间的长度的取值范围是![]() .
.
(3)先解不等式![]() ,整理,得
,整理,得![]() ,解得
,解得![]() .
.
∴不等式![]() 的解集为
的解集为![]() ,
,
设不等式![]() 的解集为B,不等式组的解集为
的解集为B,不等式组的解集为![]() ,
,
∵关于x的不等式组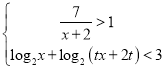 的解集构成的各区间长度和为5,且A∩B(-2,5),
的解集构成的各区间长度和为5,且A∩B(-2,5),
不等式![]() 等价于
等价于 ,
,
当时![]() ,恒成立
,恒成立
当![]() 时,不等式
时,不等式![]() 恒成立,得
恒成立,得![]() ,
,
当![]() 时,不等式
时,不等式![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,
,
∴实数![]() ,
,
综上所述,t的取值范围为![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某次文艺汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,如下表:

如果A、B两个节目要相邻,且都不排在第3号位置,则节目单上不同的排序方式有( )种
A. 192 B. 144 C. 96 D. 72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的各项为正数,且
的各项为正数,且![]() ,数列
,数列![]() 满足:
满足:![]() 对任意
对任意![]() 恒成立,且常数
恒成立,且常数![]() .
.
(1)若![]() 为等差数列,求证:
为等差数列,求证:![]() 也为等差数列;
也为等差数列;
(2)若![]() ,
,![]() 为等比数列,求
为等比数列,求![]() 的值(用c表示);
的值(用c表示);
(3)若![]() 且
且![]() ,令
,令![]() ,求证
,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在班级活动中,4名男生和3名女生站成一排表演节目:(写出必要的数学式,结果用数字作答)
(1)三名女生不能相邻,有多少种不同的站法?
(2)四名男生相邻有多少种不同的排法?
(3)女生甲不能站在左端,女生乙不能站在右端,有多少种不同的排法?
(4)甲乙丙三人按高低从左到右有多少种不同的排法?(甲乙丙三位同学身高互不相等)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题
①“若![]() ,则互为相反数”的逆命题;
,则互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若![]() ,则
,则![]() 有实根”的逆否命题;
有实根”的逆否命题;
④“不等边三角形的三个内角相等”的逆命题.
其中真命题为_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为别为
的左、右焦点为别为![]() 、
、![]() ,且过点
,且过点![]() 和
和![]() .
.
(1)求椭圆的标准方程;
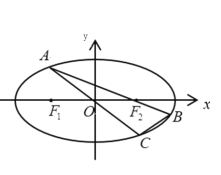
(2)如图,点![]() 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,
,![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com