
【题目】某中学调查了某班全部![]() 名同学参加学校社团的情况,数据如下表:(单位:人)
名同学参加学校社团的情况,数据如下表:(单位:人)
参加书法社 | 未参加书法社 | |
参加辩论社 |
|
|
未参加辩论社 |
|
|
(1)从该班随机选![]() 名同学,求该同学至少参加一个社团的概率;
名同学,求该同学至少参加一个社团的概率;
(2)在既参加书法社又参加辩论社的![]() 名同学中,有
名同学中,有![]() 名男同学
名男同学![]() ,
,![]() 名女同学
名女同学![]() .现从这
.现从这![]() 名同学中男女姓各随机选
名同学中男女姓各随机选![]() 人(每人被选到的可能性相同).
人(每人被选到的可能性相同).
(i)列举出所有可能结果;
(ii)设![]() 为事件“
为事件“![]() 被选中且
被选中且![]() 未被选中”,求事件
未被选中”,求事件![]() 发生的概率.
发生的概率.
科目:高中数学 来源: 题型:
【题目】高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,B、E、F为山脚两侧共线的三点,在山顶A处测得这三点的俯角分别为![]() 、
、![]() 、
、![]() ,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
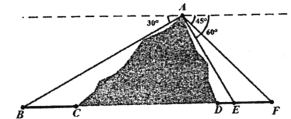
(1)求出线段AE的长度;
(2)求出隧道CD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() 上的函数
上的函数![]() ,若满足:对任意
,若满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
(1)设![]() ,判断
,判断![]() 在
在![]() 上是否有界函数,若是,请说明理由,并写出
上是否有界函数,若是,请说明理由,并写出![]() 的所有上界的值的集合,若不是,也请说明理由;
的所有上界的值的集合,若不是,也请说明理由;
(2)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为![]() ;
;
当P是原点时,定义P的“伴随点“为它自身,平面曲线C上所有点的“伴随点”所构成的曲线![]() 定义为曲线C的“伴随曲线”.现有下列命题:
定义为曲线C的“伴随曲线”.现有下列命题:
①若点A的“伴随点”是点![]() ,则点
,则点![]() 的“伴随点”是点A
的“伴随点”是点A
②单位圆的“伴随曲线”是它自身;
③若曲线C关于x轴对称,则其“伴随曲线”![]() 关于y轴对称;
关于y轴对称;
④一条直线的“伴随曲线”是一条直线.
其中的真命题是_____________(写出所有真命题的序列).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王先生购买了一部手机,欲使用中国移动“神州行”卡或加入联通的![]() 网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
网络 | 月租费 | 本地话费 | 长途话费 |
甲:联通 |
|
|
|
乙:移动“神州行” | 无 |
|
|
若王先生每月拨打本地电话的时间是拨打长途电话时间的![]() 倍,若要用联通
倍,若要用联通![]() 应最少打多长时间的长途电话才合算.( )
应最少打多长时间的长途电话才合算.( )
A.![]() 秒B.
秒B.![]() 秒C.
秒C.![]() 秒D.
秒D.![]() 秒
秒
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 且
且![]() ,
,![]() 且
且![]() ,函数
,函数![]() .
.
(1)设![]() ,
,![]() ,若
,若![]() 是奇函数,求
是奇函数,求![]() 的值;
的值;
(2)设![]() ,
,![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(3)设![]() ,
,![]() ,
,![]() ,函数
,函数![]() 的图象是否关于某垂直于
的图象是否关于某垂直于![]() 轴的直线对称?如果是,求出该对称轴,如果不是,请说明理由.
轴的直线对称?如果是,求出该对称轴,如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 是满足下列性质的函数
是满足下列性质的函数![]() 的全体,存在实数
的全体,存在实数![]()
![]() ,对于定义域内的任意
,对于定义域内的任意![]() 均有
均有![]() 成立,称数对
成立,称数对![]() 为函数
为函数![]() 的“伴随数对”.
的“伴随数对”.
(1)判断![]() 是否属于集合
是否属于集合![]() ,并说明理由;
,并说明理由;
(2)若函数![]() ,求满足条件的函数
,求满足条件的函数![]() 的所有“伴随数对”;
的所有“伴随数对”;
(3)若![]() ,
,![]() 都是函数
都是函数![]() 的“伴随数对”,当
的“伴随数对”,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .求当
.求当![]() 时,函数
时,函数![]() 的零点.
的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且点
,且点![]()
![]() 在函数
在函数![]() 的图像上;
的图像上;
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:![]() ,
,![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)在第(2)问的条件下,若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com