
【题目】在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(﹣1,0),离心率e=![]() .
.
(1)求椭圆G 的标准方程;
(2)已知直线l1:y=kx+m1与椭圆G交于 A,B两点,直线l2:y=kx+m2(m1≠m2)与椭圆G交于C,D两点,且|AB|=|CD|,如图所示.
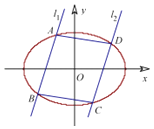
①证明:m1+m2=0;
②求四边形ABCD 的面积S 的最大值.
【答案】(1)![]() (2)①见解析②
(2)①见解析②![]()
【解析】试题分析:(1)由焦点坐标及离心率可求得![]() ,即可求椭圆G 的标准方程;(2)①利用弦长公式及韦达定理,表示出由
,即可求椭圆G 的标准方程;(2)①利用弦长公式及韦达定理,表示出由![]() ,由
,由![]() 得到
得到![]() ;②四边形
;②四边形![]() 是平行四边形,设
是平行四边形,设![]() 间的距离
间的距离![]() ,由
,由![]() 得
得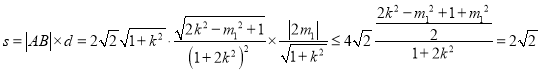 ,即可.
,即可.
试题解析:(1)设椭圆G的方程为![]() (a>b>0)
(a>b>0)
∵左焦点为F1(﹣1,0),离心率e=![]() .∴c=1,a=
.∴c=1,a=![]() ,
,
b2=a2﹣c2=1
椭圆G 的标准方程为:![]() .
.
(2)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4)
①证明:由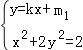 消去y得(1+2k2)x2+4km1x+2m12﹣2=0
消去y得(1+2k2)x2+4km1x+2m12﹣2=0
![]() ,
,
x1+x2=![]() ,x1x2=
,x1x2=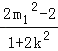 ;
;
|AB|=![]() =2
=2![]()
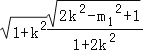 ;
;
同理|CD|=2![]()
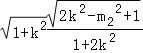 ,
,
由|AB|=|CD|得2![]()
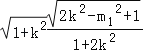 =2
=2![]()
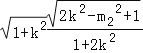 ,
,
∵m1≠m2,∴m1+m2=0
②四边形ABCD 是平行四边形,设AB,CD间的距离d=![]()
∵m1+m2=0,∴![]()
∴s=|AB|×d=2![]()
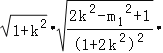 ×
×![]()
= .
.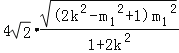
所以当2k2+1=2m12时,四边形ABCD 的面积S 的最大值为2![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的直角坐标方程,并且用
的直角坐标方程,并且用![]() (
(![]() 为直线的倾斜角,
为直线的倾斜角, ![]() 为参数)的形式写出直线
为参数)的形式写出直线![]() 的一个参数方程;
的一个参数方程;
(2) ![]() 与
与![]() 是否相交,若相交求出两交点的距离,若不相交,请说明理由.
是否相交,若相交求出两交点的距离,若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】规定投掷飞镖3次为一轮,若3次中至少两次投中8环以上为优秀,现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投标未在8环以上,用1表示该次投标在8环以上;再以每三个随机数作为一组,代表一轮的结果,经随机模拟实验产生了如下20组随机数:
101 111 011 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
据此估计,该选手投掷飞镖三轮,至少有一轮可以拿到优秀的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一生物科研小组对升高温度的多少与某种细菌种群存活数量之间的关系进行分析研究,他们制作5 份相同的样本并编号1、2、3、4、5,分别记录它们同在![]() 下升高不同的温度后的种群存活数量, 得到如下资料:
下升高不同的温度后的种群存活数量, 得到如下资料:
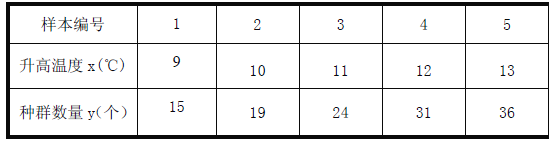
(1)若随机选取2份样本的数据来研究,求其编号不相邻的概率;
(2)求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)利用(2)中所求出的回归方程预测温度升高15 ![]() 时此种样本中种菌群存活数量.
时此种样本中种菌群存活数量.
附: 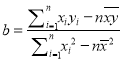 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1, ![]() 中,
中, ![]() ,点
,点![]() 为线段
为线段![]() 的四等分点,线段
的四等分点,线段![]() 互相平行,现沿
互相平行,现沿![]() 折叠得到图2所示的几何体,此几何体的底面
折叠得到图2所示的几何体,此几何体的底面![]() 为正方形.
为正方形.
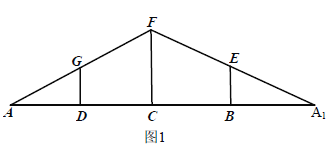

(1)证明: ![]() 四点共面;(2)求四棱锥
四点共面;(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣
x3﹣ ![]() (a∈R).
(a∈R).
(1)若a=1,求函数f(x)在[0,2]上的最大值;
(2)若对任意x∈(0,+∞),有f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点M(﹣ ![]() ),N是圆C:(x﹣
),N是圆C:(x﹣ ![]() )2+y2=16(C为圆心) 上的动点,MN的垂直平分线与NC交于点E.
)2+y2=16(C为圆心) 上的动点,MN的垂直平分线与NC交于点E.
(1)求动点E的轨迹方程C1;
(2)直线l与轨迹C1交于P,Q两点,与抛物线C2:x2=4y交于A,B两点,且抛物线C2在点A,B处的切线垂直相交于S,设点S到直线l的距离为d,试问:是否存在直线l,使得d= ![]() ?若存在,求直线l的方程;若不存在,请说明理由.
?若存在,求直线l的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com