
【题目】已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2). 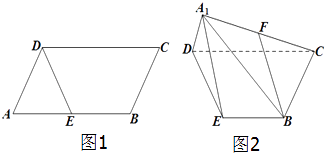
(1)求证:BF∥面A1DE;
(2)求证:面A1DE⊥面DEBC;
(3)求二面角A1﹣DC﹣E的正切值.
【答案】
(1)证明:如图,取DA1的中点G,连FG,GE;
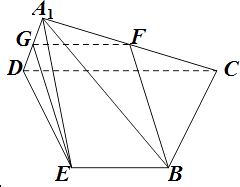 F为A1C中点;
F为A1C中点;
∴GF∥DC,且 ![]() ;
;
∴四边形BFGE是平行四边形;
∴BF∥EG,EG平面A1DE,BF平面A1DE;
∴BF∥平面A1DE
(2)证明:如图,取DE的中点H,连接A1H,CH;

AB=4,AD=2,∠DAB=60°,E为AB的中点;
∴△DAE为等边三角形,即折叠后△DA1E也为等边三角形;
∴A1H⊥DE,且 ![]() ;
;
在△DHC中,DH=1,DC=4,∠HDC=60°;
根据余弦定理,可得:
HC2=1+16﹣4=13,在△A1HC中, ![]() ,
, ![]() ,A1C=4;
,A1C=4;
∴ ![]() ,即A1H⊥HC,DE∩HC=H;
,即A1H⊥HC,DE∩HC=H;
∴A1H⊥面DEBC;
又A1H面A1DE;
∴面A1DE⊥面DEBC;
(3)解:如上图,过H作HO⊥DC于O,连接A1O;
A1H⊥面DEBC;
∴A1H⊥DC,A1H∩HO=H;
∴DC⊥面A1HO;
∴DC⊥A1O,DC⊥HO;
∴∠A1OH是二面角A1﹣DC﹣E的平面角;
在Rt△A1HO中, ![]() ,
, ![]() ;
;
故tan  ;
;
所以二面角A1﹣DC﹣E的正切值为2.
【解析】(1)取A1D中点G,并连接FG,EG,能够说明四边形BFGE为平行四边形,从而根据线面平行的判定定理即可得出BF∥面A1DE;(2)先根据已知的边、角值说明△A1DE为等边三角形,然后取DE中点H,连接CH,从而得到A1H⊥DE,根据已知的边角值求出A1H,CH,得出 ![]() ,从而得到A1H⊥CH,从而根据线面垂直及面面垂直的判定定理即可证出面A1DE⊥面DEBC;(3)过H作HO⊥DC,垂足为O,并连接A1O,容易说明DC⊥面A1HO,从而得出∠A1OH为二面角A1﹣DC﹣E的平面角,能够求出HO,从而求出tan∠A1OH,即求出了二面角A1﹣DC﹣E的正切值.
,从而得到A1H⊥CH,从而根据线面垂直及面面垂直的判定定理即可证出面A1DE⊥面DEBC;(3)过H作HO⊥DC,垂足为O,并连接A1O,容易说明DC⊥面A1HO,从而得出∠A1OH为二面角A1﹣DC﹣E的平面角,能够求出HO,从而求出tan∠A1OH,即求出了二面角A1﹣DC﹣E的正切值.
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E、F为CD上两点,且EF的长为定值,则下面四个值中不是定值的是( ) 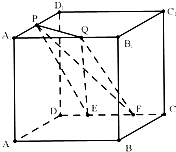
A.点P到平面QEF的距离
B.直线PQ与平面PEF所成的角
C.三棱锥P﹣QEF的体积
D.△QEF的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,点F1(﹣1,0),F2(1,0),动点M到点F2的距离是 ![]() ,线段MF1的中垂线交MF2于点P.
,线段MF1的中垂线交MF2于点P. 
(1)当点M变化时,求动点P的轨迹G的方程;
(2)设直线l:y=kx+m与轨迹G交于M、N两点,直线F2M与F2N的倾斜角分别为α、β,且α+β=π,求证:直线l经过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数序列: ![]() ,f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,fn(x)=f(fn﹣1(x)),则函数y=f2017(x)的图象与曲线
,f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,fn(x)=f(fn﹣1(x)),则函数y=f2017(x)的图象与曲线 ![]() 的交点坐标为( )
的交点坐标为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定点M(3, ![]() )与抛物线y2=2x上的点P的距离为d1 , P到抛物线准线l的距离为d2 , 则d1+d2取最小值时,P点的坐标为( )
)与抛物线y2=2x上的点P的距离为d1 , P到抛物线准线l的距离为d2 , 则d1+d2取最小值时,P点的坐标为( )
A.(0,0)
B.(1, ![]() )
)
C.(2,2)
D.( ![]() ,-
,- ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足:①f(x)+f(2﹣x)=0;②f(x﹣2)=f(﹣x),③在[﹣1,1]上表达式为f(x)= ![]() ,则函数f(x)与函数g(x)=
,则函数f(x)与函数g(x)= ![]() 的图象在区间[﹣3,3]上的交点个数为( )
的图象在区间[﹣3,3]上的交点个数为( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ﹣1(x≠0),k∈R.
﹣1(x≠0),k∈R.
(1)当k=3时,试判断f(x)在(﹣∞,0)上的单调性,并用定义证明;
(2)若对任意x∈R,不等式f(2x)>0恒成立,求实数k的取值范围;
(3)当k∈R时,试讨论f(x)的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com