练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    要得到函数的图象，只需将的图象（）
    A．向左平移个单位长度B．向右平移个单位长度
    C．向左平移个单位长度D．向右平移个单位长度
    B

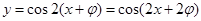
    试题分析：解：设y=cos2x平移φ个单位，得到，令，即可得到，故y=cos2x向左平移个单位得到，
    因此，要得到函数的图象，只需将的图象向右平移个单位长度．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    在平面直角坐标系xOy中，已知M是椭圆＝1上在第一象限的点，A(2，0)，B(0，2)
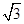
    是椭圆两个顶点，求四边形OAMB的面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

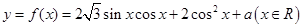
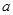
    已知函数，其中为常数．
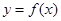
    （1）求函数的周期；
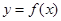
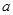
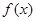
    （2）如果的最小值为，求的值，并求此时的最大值及图像的对称轴方程.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

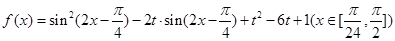
    已知其最小值为.
    （1）求的表达式；
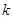
    （2）当时，要使关于的方程有一个实根，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

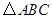
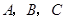
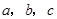
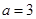
    设的内角所对的边长分别为，且，A=，．
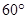
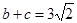
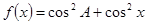
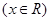
    （1）求函数的单调递增区间及最大值；
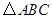
    （2）求的面积的大小

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知的最小正周期为.
    （1）当时，求函数的最小值；
    （2）在，若,且,求的值.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知函数，．
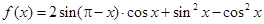
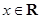
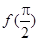
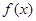
    （1）求的值及函数的最小正周期；
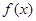
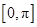
    （2）求函数在上的单调减区间．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知>0，函数f(x)=sin(x+)在(,)上单调递减，则的取值范围是（   ）
    A．[,]
    B．[,]
    C．[0,]
    D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

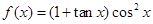
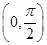
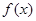
    已知函数的定义域为,则函数的值域为________.

    查看答案和解析>>

    同步练习册答案