
【题目】为参与某次救援,潜水员需潜至水下30米处进行作业.在下潜与返回水面的过程中保持匀速,速度均为![]() 米/分钟(
米/分钟(![]() ,
,![]() 为常数),下潜过程中每分钟耗氧量与速度
为常数),下潜过程中每分钟耗氧量与速度![]() 的平方成正比,当速度为1米/分钟时,每分钟耗氧量为0.2升;在水下30米作业时,每分钟耗氧量为0.4升:返回水面的过程中每分钟耗氧量为0.2升假定氧气瓶中氧气为20升,潜水员下潜时开始使用氧气瓶中的氧气,返回到水面时氧气瓶中氧气恰好用尽.
的平方成正比,当速度为1米/分钟时,每分钟耗氧量为0.2升;在水下30米作业时,每分钟耗氧量为0.4升:返回水面的过程中每分钟耗氧量为0.2升假定氧气瓶中氧气为20升,潜水员下潜时开始使用氧气瓶中的氧气,返回到水面时氧气瓶中氧气恰好用尽.
(1)试求潜水员在水下30米作业的时间![]() (单位:分钟)与速度
(单位:分钟)与速度![]() 的函数解析式;
的函数解析式;
(2)试求潜水员在水下30米能作业的最长时间.
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 是自然对数的底数)
是自然对数的底数)
(1)若![]() 在R上单调递增,求正数a的取值范围;
在R上单调递增,求正数a的取值范围;
(2)若![]() f(x)在
f(x)在![]() 处导数相等,证明:
处导数相等,证明:![]() ;
;
(3)当![]() 时,证明:对于任意
时,证明:对于任意![]() ,若
,若![]() ,则直线
,则直线![]() 与曲线
与曲线![]() 有唯一公共点(注:当
有唯一公共点(注:当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 的交点在y轴两侧).
的交点在y轴两侧).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小刘同学大学毕业后自主择业,回到农村老家发展蜜桔收购,然后卖出去,帮助村民致富.小刘打算利用“互联网+”的模式进行销售.为了更好地销售,假设该村每颗蜜柚树结果50个,现随机选了两棵树的蜜柚摘下来进行测重,其质量分布在区间内(单位:千克)的个数:![]() ,10;
,10;![]() ,10;
,10;![]() ,15;
,15;![]() ,40;
,40;![]() ,20;
,20;![]() ,5.
,5.
(1)作出其频率分布直方图并求其众数;
(2)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该村蜜袖树上大约还有100颗树的蜜柚待出售,小刘提出两种收购方案:

A.所有蜜柚均以16元/千克收购;
B.低于2.25千克的蜜柚以22元/个收购,高于或等于2.25千克的以30元/个收购.请你通过计算为该村选择收益最好的方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD中,PC⊥底面ABCD,PC=CD=2,E为AB的中点,底面四边形ABCD满足∠ADC=∠DCB=90°,AD=1,BC=3.
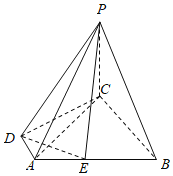
(Ⅰ)求证:平面PDE⊥平面PAC;
(Ⅱ)求直线PC与平面PDE所成角的正弦值;
(Ⅲ)求二面角D﹣PE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,连接
两点,连接![]() 并延长交
并延长交![]() 于
于![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书甲、乙、丙三人在理论考试中“合格”的概率依次为![]() ,
,![]() ,
,![]() ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为![]() ,
,![]() ,
,![]() ,所有考试是否合格相互之间没有影响.
,所有考试是否合格相互之间没有影响.
(1)假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
(2)这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于某设备的使用年限![]() (年)和所支出的维修费
(年)和所支出的维修费![]() (万元)有如下统计资料:
(万元)有如下统计资料:

若由资料知,![]() 对
对![]() 呈线性相关关系.
呈线性相关关系.
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)估计使用年限为10年时,维修费用约是多少?(精确到两位小数);
(3)计算第2年和第6年的残差.
附:回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com