
����Ŀ��������ǵĻ�������������ḻ�����˿��Ժܷ�������������Ͻ�����Ҳ��ʼ��Ϊ�������ճ������в��ɻ�ȱ��һ����.Ϊ�˽�����������![]() �е��ռ������
�е��ռ������ ![]() ��ij�������������������˹��������������ʾ����飬���Ӳ������������г�ȡ��200�˽��г����������õ�������λ���ˣ�
��ij�������������������˹��������������ʾ����飬���Ӳ������������г�ȡ��200�˽��г����������õ�������λ���ˣ�
����ʹ���������� | ż�������������� | �ϼ� | |
���� | 50 | 50 | 100 |
�� | 60 | 40 | 100 |
�ϼ� | 110 | 90 | 200 |
��1�����ݱ������ݣ��ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ
��ǰ������Ϊ![]() ��ʹ������������������Ա��йأ�
��ʹ������������������Ա��йأ�
��2�����ִ�����ȡ��Ů���������÷ֲ�����ķ����ٳ�ȡ5�ˣ��ٴ���5�������ѡ��3�����������Ż�ȯ����ѡ����3����������2�˾���ʹ�����������ĸ��ʣ�
�ڽ�Ƶ����Ϊ���ʣ���![]() �����в������������������ȡ10��������Ʒ�������о���ʹ����������������Ϊ
�����в������������������ȡ10��������Ʒ�������о���ʹ����������������Ϊ![]() ����
����![]() ����ѧ�����ͷ���.
����ѧ�����ͷ���.
�ο���ʽ��  ������
������![]() .
.
�ο����ݣ�
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
���𰸡�(1)�����ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ����������������Ա��йأ�
��ʹ����������������Ա��йأ�
(2)��![]() ���ڴ𰸼�����.
���ڴ𰸼�����.
�����������������
(1)������������������ɵÿ�֪![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]()
![]() �����Բ����ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ
�����Բ����ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ����������������Ա��йأ�
��ʹ����������������Ա��йأ�
(2)��������ɵþ���ʹ��������������![]() �ˣ�ż������������������
�ˣ�ż������������������![]() ��.��ѡ����3����������2�˾���ʹ�����������ĸ���Ϊ
��.��ѡ����3����������2�˾���ʹ�����������ĸ���Ϊ![]() .
.
��������ɵã�����������Ӷ���ֲ�![]() ����
����![]() ��
�� ![]() .
.
���������
��1������������֪![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]()
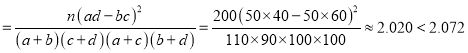 ��
��
���Բ����ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ����������������Ա��й�.
��ʹ����������������Ա��й�.
��2���������⣬��֪����ȡ��5��Ů�����У�����ʹ��������������![]() ���ˣ���
���ˣ���
ż������������������![]() ���ˣ�.��
���ˣ�.��
��ѡ����3����������2�˾���ʹ�����������ĸ���Ϊ![]() .
.
����![]() ����������֪�鵽����ʹ����������������ĸ���Ϊ
����������֪�鵽����ʹ����������������ĸ���Ϊ![]() ��
��
��Ƶ����Ϊ���ʣ�����![]() �������������ȡ1�ˣ�ǡ�ó鵽����ʹ����������������ĸ���Ϊ
�������������ȡ1�ˣ�ǡ�ó鵽����ʹ����������������ĸ���Ϊ![]() .
.
�������![]() ����
����![]() ��
�� ![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}��ǰn���ΪSn �� ������Sn=2��an �� n=1��2��3������
��1��������{an}��ͨ�ʽ��
��2��������{bn}����b1=1����bn+1=bn+an �� ������{bn}��ͨ�ʽ��
��3����cn=n��3��bn����������{cn}��ǰn���ΪTn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У� ![]() .
.
����֤���� ![]() ��
��
����ƽ��![]()
![]() ƽ��
ƽ��![]() ��
�� ![]() ����ֱ��
����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���Ϊ0�ĵȲ�����![]() ��ǰ�����Ϊ6����
��ǰ�����Ϊ6����![]() �ɵȱ�������
�ɵȱ�������
��1��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ������
������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����ʹ
����ʹ![]() ��
��![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У���ACB=90�㣬SA��ƽ��ABC��AD��SC����֤�� 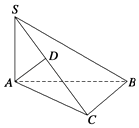
��1��BC��ƽ��SAC��
��2��AD��ƽ��SBC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��=2sin2x��ͼ������ƽ�� ![]() ����λ��õ�����g��x����ͼ��������g��x��������[0��
����λ��õ�����g��x����ͼ��������g��x��������[0�� ![]() ]��[2a��
]��[2a�� ![]() ]�Ͼ�������������ʵ��a��ȡֵ��Χ�ǣ� ��
]�Ͼ�������������ʵ��a��ȡֵ��Χ�ǣ� ��
A.[ ![]() ��
�� ![]() ]
]
B.[ ![]() ��
�� ![]() ]
]
C.[ ![]() ��
�� ![]() ]
]
D.[ ![]() ��
�� ![]() ]
]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������V��ABC�У�ƽ��VAB��ƽ��ABC����VABΪ�ȱ������Σ�AC��BC��AC=BC= ![]() ��O��M�ֱ�ΪAB��VA���е㣮
��O��M�ֱ�ΪAB��VA���е㣮 
��1����֤��VB��ƽ��MOC��
��2����֤��ƽ��MOC��ƽ��VAB
��3��������V��ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��ij��Ƹ���ϣ���5�����������Ƶ���ְ�ߣ������Ǽ�ΪA��B��C��D��E������ӦƸ���鹤������ֻ��2������ְλ�����5���н���2�˱�¼�ã����5���˱�¼�õĻ�����ȣ��ֱ���������¼��ĸ��ʣ�
��1��C�õ�һ��ְλ
��2��B��E�õ�һ��ְλ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com