
【题目】已知函数![]() ,
,![]() ,若对任意给定的
,若对任意给定的![]() ,关于
,关于![]() 的方程
的方程![]() 在区间
在区间![]() 上总存在唯一的一个解,则实数
上总存在唯一的一个解,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:由题意可以把问题转化为求函数f(x)和函数g(x)的值域,并有题意转化为两个函数的值域的关系问题.
详解:解f′(x)=6ax2﹣6ax=6ax(x﹣1),
①当a=0时,f(x)=1,g(x)=![]() ,显然不可能满足题意;
,显然不可能满足题意;
②当a>0时,f'(x)=6ax2﹣6ax=6ax(x﹣1),
x,f′(x),f(x)的变化如下:

又因为当a>0时,g(x)=﹣![]() x+
x+![]() 上是减函数,
上是减函数,
对任意m∈[0,2],g(m)∈[﹣![]() +
+![]() ,
,![]() ],
],
由题意,必有g(m)max≤f(x)max,且1﹣a>0,
故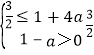 ,解得:
,解得:![]() ≤a<1,
≤a<1,
③当a<0时,g(x)=﹣![]() x+
x+![]() 上是增函数,不合题意;
上是增函数,不合题意;
综上,a∈[![]() ,1),
,1),
故选:B.


科目:高中数学 来源: 题型:
【题目】某地区某农产品近五年的产量统计如下表:

(Ⅰ)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并由所建立的回归方程预测该地区2018年该农产品的产量;
,并由所建立的回归方程预测该地区2018年该农产品的产量;
(Ⅱ)若近五年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() (单位:万吨)满足的函数关系式为
(单位:万吨)满足的函数关系式为![]() ,且每年该农产品都能售完.求年销售额
,且每年该农产品都能售完.求年销售额![]() 最大时相应的年份代码
最大时相应的年份代码![]() 的值,
的值,
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的计算公式:
的斜率和截距的计算公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)判断函数![]() 在
在![]() 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
(3)是否存在实数![]() ,对于任意
,对于任意![]() ,不等式
,不等式![]() 恒成立,若存在,求出实数
恒成立,若存在,求出实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为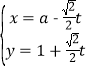 (
(![]() 为参数,
为参数,![]() ),以坐标原点为极点,以
),以坐标原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点(
两点(![]() 在
在![]() 之间),且
之间),且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的有________(只填序号)
①若直线与平面有无数个公共点,则直线在平面内;
②若直线l上有无数个点不在平面α内,则l∥α;
③若两条异面直线中的一条与一个平面平行,则另一条直线一定与该平面相交;
④若直线l与平面α平行,则l与平面α内的直线平行或异面;
⑤若平面α∥平面β,直线aα,直线bβ,则直线a∥b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子![]() 米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子
米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子![]() 米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过
米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过![]() 个直道与弯道的交接口
个直道与弯道的交接口![]() .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为![]() ,摔倒的概率均为
,摔倒的概率均为![]() .假定运动员只有在摔倒或到达终点时才停止滑行,现在用
.假定运动员只有在摔倒或到达终点时才停止滑行,现在用![]() 表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
(1)求该运动员停止滑行时恰好已顺利通过![]() 个交接口的概率;
个交接口的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com