
| A. | (1,ln2) | B. | $({\frac{1}{e},e})$ | C. | $({0,\frac{1}{e}})$ | D. | (0,e) |
分析 分离参数得k=$\frac{lnx}{x}$,作出f(x)=$\frac{lnx}{x}$的函数图象,根据函数图象即可得出k的范围.
解答 解:由kx-lnx=0得k=$\frac{lnx}{x}$,
令f(x)=$\frac{lnx}{x}$,则f′(x)=$\frac{1-lnx}{{x}^{2}}$,
∴当0<x<e时,f′(x)>0,当x>e时,f′(x)<0,
∴f(x)在(0,e)上单调递增,在(e,+∞)单调递减,
∴当x=e时,f(x)取得最大值f(e)=$\frac{1}{e}$.
作出f(x)的函数图象如图所示:
∵方程kx-lnx=0有两个实数根,即方程k=f(x)有两解,
∴0<k<$\frac{1}{e}$.
故选C.
点评 本题考查了函数零点与函数图象的关系,函数单调性与函数最值的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\stackrel{→}{AC}$ | B. | $\stackrel{→}{BD}$ | C. | $\stackrel{→}{CA}$ | D. | $\stackrel{→}{DB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在公路MN两侧分别有A1,A2,…,A7七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
如图,在公路MN两侧分别有A1,A2,…,A7七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )| A. | ① | B. | ② | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
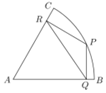 如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.
如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [6,+∞) | B. | (-∞,-6]∪[6,+∞) | C. | (6,+∞) | D. | (-6,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com