练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设等比数列{an}的前n项和为Sn，且S3=2，S6=6，则a13+a14+a15的值是（　　）
    A、18B、28C、32D、144
    考点：等比数列的前n项和
    专题：等差数列与等比数列
    分析：由等比数列性质，知S3，S6-S3，S9-S6，S12-S9，S15-S12也成等比数列，由此能求出a13+a14+a15=S15-S12=32．
    解答： 解：由等比数列性质，
    知S3，S6-S3，S9-S6，S12-S9，S15-S12也成等比数列，
    ∵S3=2，S6=6，
    ∴S3=2，S6-S3=4，S9-S6=8，S12-S9=16，S15-S12=32．
    ∴a13+a14+a15=S15-S12=32．
    故选：C．
    点评：本题考查等比数列中三项和的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    三棱柱ABC-A1B1C1各顶点都在一个球面上，侧棱与底面垂直，∠ACB=120°，CA=CB=2
    		3
    ，AA1=4，则这个球的表面积为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，a2-c2=2b，且4cosAsinC=sinB．
    （1）求b；
    （2）若S△ABC=2
    		3
    ，求△ABC的周长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面，BC=2
    		2
    ，M为BC的中点
    （Ⅰ）试在棱AD上找一点N，使得CN∥平面AMP，并证明你的结论．
    （Ⅱ）证明：AM⊥PM．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    e，π分别是自然对数的底数和圆周率，则下列不等式中不成立的是（　　）
    A、logπe+（lnπ）2＞2
    B、logπe+ln
    		π
    ＞1
    C、π-e＞eπ-ee
    D、
    2
    1
    e
    +
    1
    π
    ＜
    		eπ

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    命题“?x∈（0，+∞），
    1
    3
    x3-x+1”＞0的否定是（　　）
    A、?x0∉（0，+∞），
    1
    3
    x03-x0+1≤0
    B、?x0∈（0，+∞），
    1
    3
    x03-x0+1≤0
    C、?x0∉（0，+∞），
    1
    3
    x03-x+1≤0
    D、?x0∈（0，+∞），
    1
    3
    x3-x+1≤0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

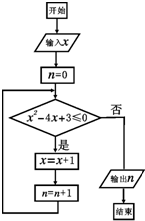    在区间[-2，3]上随机选取一个数M，不变执行如图所示的程序框图，且输入x的值为1，然后输出n的值为N，则M≤N-2的概率为（　　）
    A、
    1
    5
    B、
    2
    5
    C、
    3
    5
    D、
    4
    5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知（1+2i）（1-ai）=5（i为虚数单位），则实数a的值为（　　）
    A、-1B、1C、2D、-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sinx+2cosy=2，求cosx+2siny的范围．

    查看答案和解析>>

    同步练习册答案