
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)设线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求△
,求△![]() 的面积
的面积![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |

(1)补全频率分布直方图并求![]() 的值(直接写结果);
的值(直接写结果);
(2)从年龄段在![]() 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在![]() 岁的概率.
岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.

(I)根据直方图估计这个开学季内市场需求量![]() 的众数和中位数;
的众数和中位数;
(II)将![]() 表示为
表示为![]() 的函数;
的函数;
(III)根据直方图估计利润![]() 不少于4800元的概率.
不少于4800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,圆
,圆![]() 的圆心在圆
的圆心在圆![]() 的内部,且直线
的内部,且直线![]() 被圆
被圆![]() 所截得的弦长为
所截得的弦长为![]() .点
.点![]() 为圆
为圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求证:![]() 为定值;
为定值;
(3)当![]() 取得最大值时,求
取得最大值时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国“一带一路”战略构思提出后, 某科技企业为抓住“一带一路”带来的机遇, 决定开发生产一款大型电子设备, 生产这种设备的年固定成本为![]() 万元, 每生产
万元, 每生产![]() 台,需另投入成本
台,需另投入成本![]() (万元), 当年产量不足
(万元), 当年产量不足![]() 台时,
台时,![]() (万元); 当年产量不小于
(万元); 当年产量不小于![]() 台时
台时![]() (万元), 若每台设备售价为
(万元), 若每台设备售价为![]() 万元, 通过市场分析,该企业生产的电子设备能全部售完.
万元, 通过市场分析,该企业生产的电子设备能全部售完.
(1)求年利润![]() (万元)关于年产量
(万元)关于年产量![]() (台)的函数关系式;
(台)的函数关系式;
(2)年产量为多少台时 ,该企业在这一电子设备的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
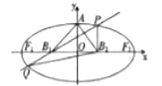
【题目】如图,设椭圆的中心为原点![]() ,长轴在
,长轴在![]() 轴上,上顶点为
轴上,上顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,线段
,线段![]() 的中点分别为
的中点分别为![]() ,且
,且![]() 是面积为
是面积为![]() 的直角三角形.
的直角三角形.
(1)求该椭圆的离心率和标准方程;
(2)过![]() 作直线交椭圆于
作直线交椭圆于![]() 两点,使
两点,使![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产![]() 产品的年固定成本为250万元,每生产
产品的年固定成本为250万元,每生产![]() 千件需另投入成本
千件需另投入成本![]() 万元,当年产量不足80千件时
万元,当年产量不足80千件时![]() (万元);当年产量不小于80千件时
(万元);当年产量不小于80千件时![]() (万元),每千件产品的售价为50万元,该厂生产的产品能全部售完.
(万元),每千件产品的售价为50万元,该厂生产的产品能全部售完.
(1)写出年利润![]() 万元关于
万元关于![]() (千件)的函数关系;
(千件)的函数关系;
(2)当年产量为多少千件时该厂当年的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂近期要生产一批化工试剂,经市场调查得知,生产这批试剂厂家的生产成本有以下三个部分:①生产1单位试剂需要原料费50元;②支付所有职工的工资总额由7500元的基本工资和每生产1单位试剂补贴所有职工20元组成;③后续保养的平均费用是每单位![]() 元(试剂的总产量为
元(试剂的总产量为![]() 单位,
单位,![]() ).
).
(1)把生产每单位试剂的成本表示为![]() 的函数关系
的函数关系![]() ,并求
,并求![]() 的最小值;
的最小值;
(2)如果产品全部卖出,据测算销售额![]() (元)关于产量
(元)关于产量![]() (单位)的函数关系为
(单位)的函数关系为![]() ,试问:当产量为多少时生产这批试剂的利润最高?
,试问:当产量为多少时生产这批试剂的利润最高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com