
【题目】已知函数![]() (
(![]() 为自然对数的底数)有两个极值点,则实数
为自然对数的底数)有两个极值点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)设![]() ,求证:数列
,求证:数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对于
对于![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要分析学生初中升学考试的数学成绩对高一年级数学学习有什么影响,在高一年级学生中随机抽取10名学生,分析他们入学的数学成绩(x)和高一年级期末数学考试成绩(y)(如下表):
(1)画出散点图;
(2)判断入学成绩(x)与高一期末考试成绩(y)是否有线性相关关系;
(3)如果x与y具有线性相关关系,求出回归直线方程;
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
y | 65 | 78 | 52 | 85 | 92 | 89 | 73 | 98 | 56 | 75 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
车间 | A | B | C |
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点
),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,若点
上一点,若点![]() 到曲线
到曲线![]() 的最小距离为
的最小距离为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示.以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )
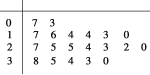

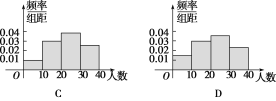
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com