
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)设函数![]() ,其中
,其中![]() .若函数
.若函数![]() 与
与![]() 的图象有且只有一个交点,求
的图象有且只有一个交点,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]() ;(2)
;(2) ![]()
【解析】试题分析:(1)由![]() 化简可得
化简可得![]() 恒成立,从而可求出
恒成立,从而可求出![]() 的值; (2)先利用对数的运算法则对不等式化简,再根据对数函数的单调性及指数函数的性质解不等式;(3)运用函数与方程思想解题,问题转化为关于
的值; (2)先利用对数的运算法则对不等式化简,再根据对数函数的单调性及指数函数的性质解不等式;(3)运用函数与方程思想解题,问题转化为关于![]() 的方程
的方程![]() 在
在![]() 上只有一解,分两种情况讨论,利用二次函数的性质列不等式求解即可.
上只有一解,分两种情况讨论,利用二次函数的性质列不等式求解即可.
试题解析:(1)![]() 是偶函数,
是偶函数,
![]() 对任意
对任意![]() ,恒成立
,恒成立
![]() 恒成立,
恒成立,
![]() 恒成立
恒成立
![]()
(2)若![]() 则
则![]()
所以![]() ,所以
,所以![]()
令![]() 则有
则有![]() 即
即![]()
解得![]() 或
或![]()
所以![]() 或
或![]()
所以![]() 或
或![]()
(3)由于![]() ,所以
,所以![]() 定义域为
定义域为![]() ,也就是满足
,也就是满足![]()
![]() 函数
函数![]() 与
与![]() 的图象有且只有一个交点,
的图象有且只有一个交点,
![]() 方程
方程![]() 在
在![]() 上只有一解
上只有一解
即:方程![]() 在
在![]() 上只有一解,令
上只有一解,令![]() ,则
,则![]() ,
,
因而等价于关于的方程![]()
![]() 在
在![]() 上只有一解
上只有一解
①当![]() 时,解得
时,解得![]() ,不合题意;
,不合题意;
当![]() 时,记
时,记![]() ,其图象的对称轴
,其图象的对称轴![]()
![]() 函数
函数![]() 在
在![]() 上递减,而
上递减,而![]() 方程
方程![]() 在
在![]() 无解
无解
②当![]() 时,记
时,记![]() ,其图象的对称轴
,其图象的对称轴![]() ,
, ![]() ,所以,只需
,所以,只需![]() ,
,
即![]() ,此恒成立
,此恒成立![]() 此时
此时![]() 的范围为
的范围为![]()
综上所述,所求![]() 的取值范围为
的取值范围为![]()


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1、F2 , 焦距为2,过点F2作直线l交椭圆于M、N两点,△F1MN的周长为8.
=1(a>b>0)的左、右焦点分别为F1、F2 , 焦距为2,过点F2作直线l交椭圆于M、N两点,△F1MN的周长为8. 
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l分别交直线y= ![]() x,y=﹣
x,y=﹣ ![]() x于P,Q两点,求
x于P,Q两点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有某批次同一型号的产品共10件,其中有8件合格品,2件次品.
(Ⅰ)某检验员从中有放回地连续抽取产品2次,每次随机抽取1件,求两次都取到次品的概率;
(Ⅱ)若该检验员从中任意抽取2件,用X表示取出的2件产品中次品的件数,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:他们研究过图(1)中的1,3,6,10,…,由于这些数能够表示成三角形,所以将其称为三角形数;类似地,称图(2)中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )


A. 289 B. 1 024
C. 1 225 D. 1 378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(﹣1)=0,当x>0时,xf′(x)﹣f(x)<0,则使得f(x)>0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(﹣1,0)
D.(0,1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,曲线C1的参数方程为 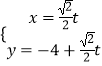 (t为参数),在极坐标系(以坐标原点O为极点,x轴的正半轴为极轴)中,曲线C2的方程为ρsin2θ=2pcosθ(p>0),曲线C1、C2交于A、B两点.
(t为参数),在极坐标系(以坐标原点O为极点,x轴的正半轴为极轴)中,曲线C2的方程为ρsin2θ=2pcosθ(p>0),曲线C1、C2交于A、B两点.
(Ⅰ)若p=2且定点P(0,﹣4),求|PA|+|PB|的值;
(Ⅱ)若|PA|,|AB|,|PB|成等比数列,求p的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标是ρ=2asinθ,直线l的参数方程是 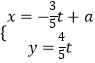 (t为参数).
(t为参数).
(1)若a=2,M为直线l与x轴的交点,N是圆C上一动点,求|MN|的最大值;
(2)若直线l被圆C截得的弦长为 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度![]() (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度![]() (单位:辆/千米)
(单位:辆/千米)
的函数.当桥上的车流密度达到200辆/千米时,就会造成堵塞,此时车流速度为0;当
车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当![]() 时,
时,
车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)如果车流量(单位时间内通过桥上某观测点的车辆数)![]() (单位:辆/小时),那么当车流密度
(单位:辆/小时),那么当车流密度![]() 为多大时,车流量
为多大时,车流量![]() 可以达到最大,并求出最大值.(精确到
可以达到最大,并求出最大值.(精确到![]() 辆/小时).
辆/小时).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com