练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．画出下列函数的简图．
    （1）y=$\frac{x+1}{x}$；
    （2）y=1-$\frac{1}{x-1}$．

    分析 利用图象变换，即可画出函数的简图．

    解答 解：（1）y=$\frac{x+1}{x}$=1+$\frac{1}{x}$的图象是由y=$\frac{1}{x}$的图象向上平移1个单位得到，如图1所示；
    （2）y=1-$\frac{1}{x-1}$的图象是由y=-$\frac{1}{x}$的图象先向右平移1个单位，再向上平移1个单位得到，如图2所示．

    点评 本题考查函数图象的作法，考查函数的化简，正确运用图象变换是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．已知数列{an}的前n项和为Sn，且a1=1，an+1=$\frac{1}{2}$Sn（n=1，2，3，…）．则数列{an}的通项公式为an=$\left\{\begin{array}{l}{1，n=1}\\{\frac{1}{2}×（\frac{3}{2}）^{n-2}，n≥2}\end{array}\right.$．n∈N*．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知直线l：y=kx+1与圆C：（x-2）2+（y-3）2=1相交于A，B两点
    （1）求弦AB的中点M的轨迹方程；
    （2）若O为坐标原点，S（k）表示△OAB的面积，若f（k）=[S（k）•（k2+1）]2，求f（k）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设D、E是△ABC所在平面内不同的两点，且$\overrightarrow{AD}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$，则△ABE和△ABD的面积比$\frac{{S}_{△ABE}}{{S}_{△ABD}}$为（　　）
    A．$\frac{1}{3}$B．$\frac{2}{3}$C．$\frac{3}{4}$D．$\frac{4}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知命题p：函数f（x）=|cosx|的最小正周期为2π；命题q：?x，使2x＞3x，则下列命题是真命题的是（　　）
    A．p∧qB．p∧（￢q）C．p∨（￢q）D．p∨q

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年江苏泰兴中学高二上学期期末数学（文）试卷（解析版） 题型：解答题

    根据统计资料，某工艺品厂的日产量最多不超过20件根据统计资料，每日产品废品率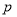与日产量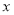（件）之间近似地满足关系式（日产品废品率=×100％） ．已知每生产一件正品可赢利2千元，而生产一件废品则亏损1千元．（该车间的日利润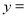日正品赢利额日废品亏损额）

    （1）将该车间日利润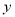（千元）表示为日产量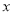（件）的函数；

    （2）当该车间的日产量为多少件时，日利润最大？最大日利润是几千元？

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年江苏泰兴中学高二上学期期末数学（文）试卷（解析版） 题型：填空题

    设函数的导数为，且，则 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

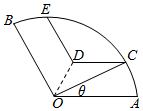    8．如图，扇形AOB是一个植物园的平面示意图，其中∠AOB=$\frac{2π}{3}$，半径OA=OB=1km，为了便于游客观赏，拟在圆内铺设一条从入口A到出口B的观赏道路，道路由弧$\widehat{AC}$，线段CD，线段DE和弧$\widehat{EB}$组成，且满足：$\widehat{AC}$=$\widehat{EB}$，CD∥AO．DE∥OB，OD∈[$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{6}}{3}$]（单位：km），设∠AOC=θ．
    （1）用θ表示CD的长度，并求出θ的取值范围；
    （2）当θ为何值时，观赏道路最长？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知集合M和N间的关系为M∩N=M，那么下列必定成立的是（　　）
    A．∁UN∩M=∅B．∁UM∩N=∅C．∁UM∩∁UN=∅D．∁UM∪∁UN=∅

    查看答案和解析>>

    同步练习册答案