
 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分. ,故可看作独立重复试验,故
,故可看作独立重复试验,故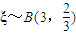 ,
,
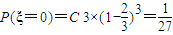 ,
,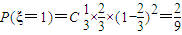 ,
,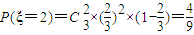 ,
,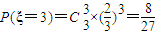 .
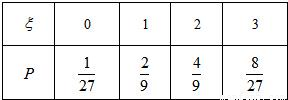
.
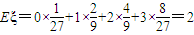 .
.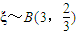 ,
,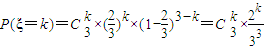 ,k=0,1,2,3.
,k=0,1,2,3.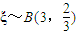 ,所以
,所以 .
.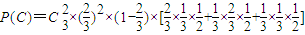 =
=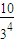 ,
,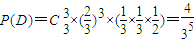 ,
,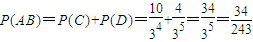 .
.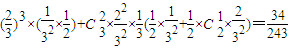 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013届广东惠阳一中实验学校高二6月月考理科数学试卷(解析版) 题型:解答题
(本题满分12分)
甲、乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,
答错得零分.假设甲队中每人答对的概率均为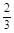 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为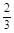 ,
,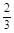 ,
, ,且各人回答正确与否相互之间没有影响.用
,且各人回答正确与否相互之间没有影响.用 表示甲队的总得分.
表示甲队的总得分.
(1)求 的概率及
的概率及 的数学期望
的数学期望 ;
;
(2)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求 .
.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省温州市八校联考高三(上)入学数学试卷(理科)(解析版) 题型:解答题
 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为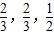 ,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.查看答案和解析>>
科目:高中数学 来源:2008年山东省高考数学试卷(理科)(解析版) 题型:解答题
 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为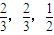 ,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com