【题目】已知动圆过定点
，且与直线
相切．
（1）求动圆圆心的轨迹
的方程；
（2）过（1）中轨迹
上的点
作两条直线分别与轨迹
相交于
两点，试探究：当直线
的斜率存在且倾斜角互补时，直线
的斜率是否为定值？若是，求出这个定值；若不是，请说明理由．
【答案】（1）
；（2）
．
【解析】
试题分析：（1）由题及抛物线的定义知，轨迹
是以定点
为焦点，直线
为准线的抛物线，即可求解点
的轨迹方程；（2）设直线
的斜率为
，则直线
的斜率为
，代入抛物线的方程，求出
的纵坐标，表示直线
的斜率，即可求得结论．
试题解析：（1）由题及抛物线的定义知，轨迹是以定点为焦点，直线为准线的抛物线，∴
，∴
，即轨迹
．．．．．．．．．．．．．．．．．．4分
（2）由题知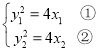
，
由①—②得
，
∴
．．．．．．．．．．．．．．．．．．．．．．6分
设直线的斜率为，则直线的斜率为，
∴
，则由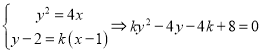
，
∴
，∴
，
同理得
．．．．．．．．．．．．．．．．．．．．．10分
∴
，
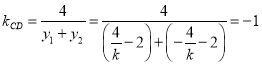即直线
的斜率为定值．．．．．．．．．．．．．．．．．．．．．．．．．．12分
口算题卡北京妇女儿童出版社系列答案科目：高中数学 来源： 题型：
【题目】已知数列
满足：对于任意
且
时，
，
．
（1）若
，求证：
为等比数列；
（2）若
．
① 求数列的通项公式；
② 是否存在
，使得
为数列中的项？若存在，求出所有满足条件的
的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图．
(2)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
.
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤．
(参考数值：3×2.5＋4×3＋5×4＋6×4.5＝66.5)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的一个焦点与短轴的两个端点是正三角形的三个项点，点
在椭圆
上．
（1）求椭圆
的方程；
（2）设不过原点
且斜率为
的直线
与椭圆
交于不同的两点
，线段
的中点为
，直线
与椭圆
交于
，证明：
．
查看答案和解析>>
科目：高中数学 来源： 题型：
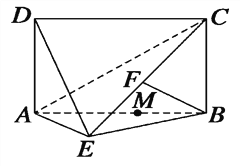
【题目】如图，四边形ABCD为矩形，DA⊥平面ABE，AE＝EB＝BC＝2，
BF⊥平面ACE，且点F在CE上．
(1)求证：AE⊥BE；
(2)求三棱锥D—AEC的体积；
(3)设点M在线段AB上，且满足AM＝2MB，试在线段CE上确定一点N，
使得MN∥平面DAE.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某生态园将一三角形地块
的一角
开辟为水果园种植桃树，已知角
为
,
的长度均大于
米，现在边界
处建围墙，在
处围竹篱笆．
（1）若围墙
总 长度为米，如何围可使得三角形地块
的面积最大？
（2）已知
段围墙高
米，
段围墙高
米，造价均为每平方米
元．若围围墙用了
元,问如何围可使竹篱笆用料最省？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
为原点的直角坐标系中，点
为
的直角顶点，已知
，且点
的纵坐标大于0．
(1)求
的坐标；
(2)求圆
关于直线
对称的圆
的方程；在直线上是否存在点
，过点的任意一条直线如果和圆
圆都相交，则该直线被两圆截得的线段长相等，如果存在求出点的坐标，如果不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
