
【题目】已知椭圆C: ![]() (a>b>0)经过点(
(a>b>0)经过点(![]() ,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.
,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点(-1,0)的直线l与椭圆C相交于A,B两点,试问在x轴上是否存在一个定点M,使得![]() 恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
【答案】(Ⅰ) ![]() (Ⅱ)-
(Ⅱ)-![]() .
.
【解析】试题分析:(Ⅰ) 由以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点可知![]() ,将点
,将点![]() 代入椭圆方程,即可求得
代入椭圆方程,即可求得![]() 和
和![]() 的值,从而求得椭圆方程;(Ⅱ) 分类讨论,当斜率存在时,将直线方程代入椭圆方程,由韦达定理及向量数量积的坐标运算,及
的值,从而求得椭圆方程;(Ⅱ) 分类讨论,当斜率存在时,将直线方程代入椭圆方程,由韦达定理及向量数量积的坐标运算,及![]() 恒为定值即可求得
恒为定值即可求得![]() 的值,从而求得
的值,从而求得![]() 的值及
的值及![]() 点坐标;当直线
点坐标;当直线![]() 的斜率
的斜率![]() 不存在时,点
不存在时,点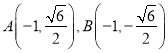 ,则
,则![]() 时,求得
时,求得![]() 的值及
的值及![]() 点坐标.
点坐标.
试题解析:(Ⅰ)由题意可得圆的方程为x2+y2=b2.因为该圆经过椭圆的焦点,所以半焦距c=b,所以a2=2b2.将点(![]() ,1)代入椭圆方程
,1)代入椭圆方程![]() 可得b2=2,a2=4,
可得b2=2,a2=4,
所以椭圆C的方程为![]() .
.
(Ⅱ)设点A(x1,y1),B(x2,y2),M(m,0).
当直线l的斜率k存在时,设直线l的方程为y=k(x+1).
联立![]() 得(1+2k2)x2+4k2x+2k2-4=0,
得(1+2k2)x2+4k2x+2k2-4=0,
则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
又y1y2=k2(x1+1)(x2+1)=k2(x1x2+x1+x2+1)=k2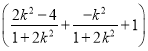 =
=![]() ,
,
而![]() =(x1-m)(x2-m)+y1y2=
=(x1-m)(x2-m)+y1y2=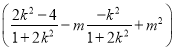 +
+![]()
=![]()
=![]() 为定值,
为定值,
只需![]() ,解得m=-
,解得m=-![]() ,从而
,从而![]() =-
=-![]() ,
,
当直线l的斜率k不存在时,点A(-1, ![]() ),B(-1,-
),B(-1,-![]() ),
),
此时,当m=-![]() 时,
时, ![]() =(-1-m)(-1-m)-
=(-1-m)(-1-m)-![]() =-
=-![]() .
.
综上,存在点M(-![]() ,0),使得
,0),使得![]() =-
=-![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和平面向量数量积公式,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确的命题有( )
A. ①② B. ②③
C. ①③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,a10=4a3,a4=3a1+7.
(1)求通项公式an;
(2)若bn=an-2an+2,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
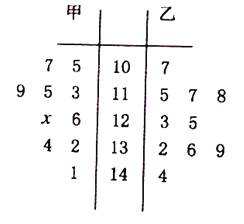
【题目】为了减少雾霾,还城市一片蓝天,某市政府于12月4日到12月31日在主城区实行车辆限号出行政策,鼓励民众不开车低碳出行,某甲乙两个单位各有200名员工,为了了解员工低碳出行的情况,统计了12月5日到12月14日共10天的低碳出行的人数,画出茎叶图如下:
(1)若甲单位数据的平均数是122,求![]() ;
;
(2)现从如图的数据中任取4天的数据(甲、乙两单位中各取2天),记其中甲、乙两单位员工低碳出行人数不低于130人的天数为![]() ,
, ![]() ,令
,令![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有两个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )
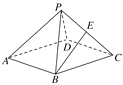
A. BE∥平面PAD,且BE到平面PAD的距离为![]()
B. BE∥平面PAD,且BE到平面PAD的距离为![]()
C. BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D. BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为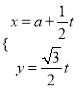
![]() .以坐标原点为极点,以
.以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于A,B两点,当
交于A,B两点,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x)万元,当年产量不足80千件时,C(x)=![]() x2+10x(万元);当年产量不少于80千件时,C(x)=51x+
x2+10x(万元);当年产量不少于80千件时,C(x)=51x+![]() -1 450(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
-1 450(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com