
【题目】某校高二年级学生会有理科生4名,其中3名男同学;文科生3名,其中有1名男同学.从这7名成员中随机抽4人参加高中示范校验收活动问卷调查.
(Ⅰ)设![]() 为事件“选出的4人中既有文科生又有理科生”,求事件
为事件“选出的4人中既有文科生又有理科生”,求事件![]() 的概率;
的概率;
(Ⅱ)设![]() 为选出的4人中男生人数与女生人数差的绝对值,求随机变量
为选出的4人中男生人数与女生人数差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
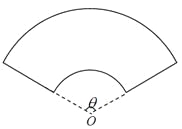
【题目】某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点![]() 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点![]() 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为![]() 米,圆心角为
米,圆心角为![]() (弧度).
(弧度).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 为何值时,
为何值时, ![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周脾算经》有记载:一年有二十四个节气,每个节气晷(gui)长损益相同,晷是按照日影测定时刻的仪器,晷长即所测定的影子的长度,二十四节气及晷长变化如图所示,相邻两个节气晷长变化量相同,周而复始,若冬至晷长最长是一丈三尺五寸,夏至晷长最短是一尺五寸,(一丈等于10尺,一尺等于10寸),则秋分节气的晷长是( )
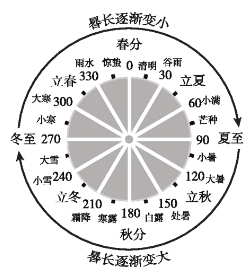
A.七尺五寸B.二尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴相切于点(0,3),圆心在经过点(2,1)与点(﹣2,﹣3)的直线
轴相切于点(0,3),圆心在经过点(2,1)与点(﹣2,﹣3)的直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)圆![]() 与圆
与圆![]() :
:![]() 相交于M、N两点,求两圆的公共弦MN的长.
相交于M、N两点,求两圆的公共弦MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知函数![]() ,函数
,函数![]() 的导函数为
的导函数为![]() .
.
①求函数![]() 的定义域;
的定义域;
②求函数![]() 的零点个数.
的零点个数.
(2)给出如下定义:如果![]() 是曲线
是曲线![]() 和曲线
和曲线![]() 的公共点,并且曲线
的公共点,并且曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 在点
在点![]() 处的切线重合,则称曲线
处的切线重合,则称曲线![]() 与曲线
与曲线![]() 在点
在点![]() 处相切,点
处相切,点![]() 叫曲线
叫曲线![]() 和曲线
和曲线![]() 的一个切点.试判断曲线
的一个切点.试判断曲线![]() :
:![]() 与曲线
与曲线![]() :
:![]() 是否在某点处相切?若是,求出所有切点的坐标;若不是,请说明理由.
是否在某点处相切?若是,求出所有切点的坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com