
【题目】在等差数列{an}中,a1=﹣2,a12=20. (Ⅰ)求通项an;
(Ⅱ)若 ![]() ,求数列
,求数列 ![]() 的前n项和.
的前n项和.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(2015·陕西)已知椭圆E: ![]() (a>b>0)的半焦距为c,原点0到经过两点(c,0),(0,b)的直线的距离为
(a>b>0)的半焦距为c,原点0到经过两点(c,0),(0,b)的直线的距离为![]() c.
c.
(1)求椭圆E的离心率
(2)如图,AB是圆M:(x+2)2+(y-1)=![]() 的一条直径,若椭圆E经过A,B两点,求椭圆E的方程.
的一条直径,若椭圆E经过A,B两点,求椭圆E的方程.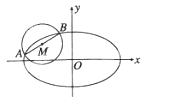
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中的内角A,B,C的对边分别为a,b,c,若 ![]() b=4c,B=2C (Ⅰ)求cosB;
b=4c,B=2C (Ⅰ)求cosB;
(Ⅱ)若c=5,点D为边BC上一点,且BD=6,求△ADC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,射线l:θ= ![]() 与圆C:ρ=2交于点A,椭圆Γ的方程为ρ2=
与圆C:ρ=2交于点A,椭圆Γ的方程为ρ2= ![]() ,以极点为原点,极轴为x轴正半轴建立平面直角坐标系xOy (Ⅰ)求点A的直角坐标和椭圆Γ的参数方程;
,以极点为原点,极轴为x轴正半轴建立平面直角坐标系xOy (Ⅰ)求点A的直角坐标和椭圆Γ的参数方程;
(Ⅱ)若E为椭圆Γ的下顶点,F为椭圆Γ上任意一点,求 ![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:mx2+y2=1(m>0).
(Ⅰ)若椭圆E的右焦点坐标为 ![]() ,求m的值;
,求m的值;
(Ⅱ)由椭圆E上不同三点构成的三角形称为椭圆的内接三角形.若以B(0,1)为直角顶点的椭圆E的内接等腰直角三角形恰有三个,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆W: ![]() (a>b>0)的上下顶点分别为A,B,且点B(0,﹣1).F1 , F2分别为椭圆W的左、右焦点,且∠F1BF2=120°.
(a>b>0)的上下顶点分别为A,B,且点B(0,﹣1).F1 , F2分别为椭圆W的左、右焦点,且∠F1BF2=120°.
(Ⅰ)求椭圆W的标准方程;
(Ⅱ)点M是椭圆上异于A,B的任意一点,过点M作MN⊥y轴于N,E为线段MN的中点.直线AE与直线y=﹣1交于点C,G为线段BC的中点,O为坐标原点.求∠OEG的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com