分析:(1)先建立空间直角坐标系,求出各点的坐标,以及向量
,
的坐标,结合
=λ,以及异面直线AC
1与CD所成角的余弦值为
,得到关于λ的等式,即可求出结论.
(2)先求两个平面法向量的坐标,再代入向量的夹角计算公式即可求出结论.
解答:解:(1)以CA,CB,CC
1分别为x,y,z轴建立如图所示空间直角坐标,
因为AC=3,BC=4,AA
1=4,所以A(3,0,0),B(0,4,0),C(0,0,0),C
1=(0,0,4),
所以
=(-3,0,4),因为
=λ,
所以点D(-3λ+3,4λ,0),所以
=(-3λ+3,4λ,0),
因为异面直线AC
1与CD所成角的余弦值为
,
所以
|cos<,>|==,解得
λ=.…(4分)
(2)由(1)得B
1(0,4,4),因为 D是AB的中点,所以
D(,2,0),
所以
=(,2,0),
=(0,4,4),平面CBB
1C
1的法向量
=(1,0,0),
设平面DB
1C的一个法向量
=(x
0,y
0,z
0),
则
,
的夹角(或其补角)的大小就是二面角D-CB
1-B的大小,
由
得
令x
0=4,则y
0=-3,z
0=3,
所以
=(4,-3,3),
∴cos<
,
>=
=
=
.
所以二面角D-B
1C-B的余弦值为
. …(10分)
点评:本题主要考察利用空间向量求平面间的夹角.解决这类题目的关键在于求两个平面法向量的坐标,再代入向量的夹角计算公式.

 附加题(必做题)
附加题(必做题)

 附加题必做题如图,正四棱柱ABCD-A1B1C1D1中,设AD=1,D1D=λ(λ>0),若棱C1C上存在点P满足A1P⊥平面PBD,求实数λ的取值范围.
附加题必做题如图,正四棱柱ABCD-A1B1C1D1中,设AD=1,D1D=λ(λ>0),若棱C1C上存在点P满足A1P⊥平面PBD,求实数λ的取值范围.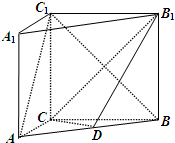
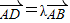 ,异面直线AC1与CD所成角的余弦值为
,异面直线AC1与CD所成角的余弦值为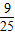 ,求λ的值;
,求λ的值;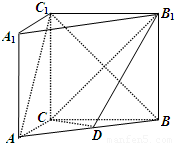
 ,异面直线AC1与CD所成角的余弦值为
,异面直线AC1与CD所成角的余弦值为 ,求λ的值;
,求λ的值;