
【题目】(题文)某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:


(1)补全频率分布直方图并求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)从![]() 岁年龄段的“低碳族”中采用分层抽样法抽取
岁年龄段的“低碳族”中采用分层抽样法抽取![]() 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取![]() 人作为领队,记选取的
人作为领队,记选取的![]() 名领队中年龄在
名领队中年龄在![]() 岁的人数为
岁的人数为![]() ,求
,求![]() 的分布列和期望
的分布列和期望![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
试题分析:(1)频率分布直方图中各小矩形的面积为该组的频率,根据各频率和为1,可得第二组的频率,从而可求得该组小矩形的高,从而可将图补充完整.根据频率等于频数除以总数由第一组可求得总数,从而可求得![]() 的值.(2)
的值.(2)![]() 岁年龄段的“低碳族”与
岁年龄段的“低碳族”与![]() 岁年龄段的“低碳族”的比值可得18人中应在各组抽取的人数.可知随机变量
岁年龄段的“低碳族”的比值可得18人中应在各组抽取的人数.可知随机变量![]() 服从超几何分布,根据超几何分布的概率公式可求得
服从超几何分布,根据超几何分布的概率公式可求得![]() .从而可得其分布列及期望值.
.从而可得其分布列及期望值.
试题解析:(1)第二组的频率为![]() ,所以高为
,所以高为![]() .
.
频率直方图如下:
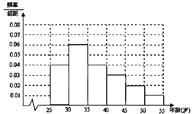
第一组的人数为![]() ,频率为
,频率为![]() ,所以
,所以![]() .
.
第二组的频率为![]() ,所以第二组的人数为
,所以第二组的人数为![]() ,所以
,所以![]() .
.
第四组的频率为![]() ,第四组的人数为
,第四组的人数为![]() ,
,
所以![]() .
.
(2)因为![]() 岁年龄段的“低碳族”与
岁年龄段的“低碳族”与![]() 岁年龄段的“低碳族”的比值为
岁年龄段的“低碳族”的比值为![]() ,所以采用分层抽样法抽取18人,
,所以采用分层抽样法抽取18人,![]() 岁中有12人,
岁中有12人,![]() 岁中有6人.
岁中有6人.
随机变量![]() 服从超几何分布.
服从超几何分布.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以随机变量![]() 的分布列为
的分布列为

∴数学期望![]() .
.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,极点为O,点A的极坐标为(2, ![]() ),以OA为斜边作等腰直角三角形OAB(其中O,A,B按逆时针方向分布)
),以OA为斜边作等腰直角三角形OAB(其中O,A,B按逆时针方向分布)
(1)求点B的极坐标;
(2)求三角形外接圆的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(0,+∞),f′(x)为f(x)的导函数,且满足xf′(x)>f(x),则不等式(x﹣1)f(x+1)>f(x2﹣1)的解集是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为迎接“国家义务教育均衡发展”综合评估,市教育行政部门在全市范围内随机抽取了![]() 所学校,并组织专家对两个必检指标进行考核评分.其中
所学校,并组织专家对两个必检指标进行考核评分.其中![]() 分别表示“学校的基础设施建设”和“学校的师资力量”两项指标,根据评分将每项指标划分为
分别表示“学校的基础设施建设”和“学校的师资力量”两项指标,根据评分将每项指标划分为![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (及格)三个等级,调查结果如表所示.例如:表中“学校的基础设施建设”指标为
(及格)三个等级,调查结果如表所示.例如:表中“学校的基础设施建设”指标为![]() 等级的共有
等级的共有![]() 所学校.已知两项指标均为
所学校.已知两项指标均为![]() 等级的概率为0.21.
等级的概率为0.21.

(1)在该样本中,若“学校的基础设施建设”优秀率是0.4,请填写下面![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 的把握认为“学校的基础设施建设”和“学校的师资力量”有关;
的把握认为“学校的基础设施建设”和“学校的师资力量”有关;
师资力量(优秀) | 师资力量(非优秀) | 合计 | |
基础设施建设(优秀) | |||
基础设施建设(非优秀) | |||
合计 |
(2)在该样本的“学校的师资力量”为![]() 等级的学校中,若
等级的学校中,若![]() ,记随机变量
,记随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地有三家工厂,分别位于矩形ABCD的顶点A,B以及CD的中点P处,已知AB=20km,CB=10km,为了处理三家工厂的污水,现要在矩形ABCD内(含边界),且与A,B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为![]() km.
km.

(I)设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
(II)确定污水处理厂的位置,使三条排污管道的总长度最短,并求出最短值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1)根据题意完成表格;
(2)是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax,a>0.
(1)记f(x)的极小值为g(a),求g(a)的最大值;
(2)若对任意实数x恒有f(x)≥0,求f(a)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有6个人排成一排照相,由于甲乙性格不合,所以要求甲乙不相邻,丙最高,要求丙站在最中间的两个位置中的一个位置上,则不同的站法有( )种.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com