练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】统计表明某型号汽车在匀速行驶中每小时的耗油量(升)关于行驶速度(千米/小时)的函数为 ．

    （1）当千米/小时时,行驶千米耗油量多少升？

    （2）若油箱有升油,则该型号汽车最多行驶多少千米？

    【答案】(1)11.95(升) ．

    (2) 千米．

    【解析】分析：（1）由题意可得当x=64千米/小时，要行驶千米需要小时，代入函数y的解析式，即可得到所求值；

    （2）设22.5升油能使该型号汽车行驶a千米，代入函数y的式子，可得．

    令，求出导数和单调区间，可得h（x）的最小值，进而得到a的最大值．

    详解：(1)当千米/小时时,要行驶千米需要小时，

    要耗油 (升) ．

    (2)设升油能使该型号汽车行驶千米,由题意得，

    ，所以 ，

    设

    则当最小时，取最大值，令

    当时，，当时，

    故当时，函数为减函数，当时，函数为增函数，

    所以当时， 取得最小值，此时取最大值为

    所以若油箱有升油,则该型号汽车最多行驶千米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数的图象在点处的切线方程为，求，的值；

    （2）当时，在区间上至少存在一个，使得成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆,圆与圆关于直线对称.

    (1)求圆的方程;

    (2)过直线上的点分别作斜率为的两条直线,使得被圆截得的弦长与被圆截得的弦长相等.

    (i)求的坐标;

    (ⅱ)过任作两条互相垂直的直线分别与两圆相交,判断所得弦长是否恒相等,并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设为直线，是两个不同的平面，下列命题中正确的是(　　)

    A. 若∥α，∥β，则α∥βB. 若⊥α，⊥β，则α∥β

    C. 若⊥α，∥β，则α∥βD. 若α⊥β，∥α，则⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，A、B、C为⊙O上三点，B为 的中点，P为AC延长线上一点，PQ与⊙O相切于点Q，BQ与AC相交于点D．
    （Ⅰ）证明：△DPQ为等腰三角形；
    （Ⅱ）若PC=1，AD=PD，求BDQD的值．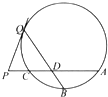

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损．某投资人打算投资甲、乙两个项目．根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损分别为30%和10%．投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元．问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x）=x3+ax2+bx（a，b∈R）的图象与x轴相切于一点A（m，0）（m≠0），且f（x）的极大值为 ，则m的值为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=ex﹣ax2﹣2x+b（e为自然对数的底数，a，b∈R）．
    （Ⅰ）设f′（x）为f（x）的导函数，证明：当a＞0时，f′（x）的最小值小于0；
    （Ⅱ）若a＜0，f（x）＞0恒成立，求符合条件的最小整数b．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的上、下焦点分别为，上焦点到直线的距离为3，椭圆的离心率.

    （1）求椭圆的方程；

    （2）椭圆，设过点斜率存在且不为0的直线交椭圆于两点，试问轴上是否存在点，使得？若存在，求出点的坐标；若不存在，说明理由.

    查看答案和解析>>

    同步练习册答案