
思路分析:若设每根截500 mm的x根、600 mm的y根,
则 即
即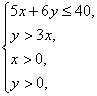
其中x、y均为正整数,
可行域如下图所示,
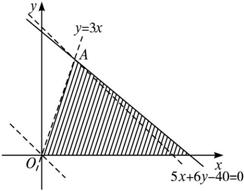
目标函数为z=x+y,作一组平行直线x+y=t,经过可行域中的点且和原点距离最远的直线为过点A的直线.
由![]() 得
得
故A(![]() ,
,![]() ),
),
调整为x=2,y=5,即x+y=7,经检验满足条件.
∴每根截500 mm的2根、600 mm的5根合理.
但这是错误的.
上述解法错误的原因是满足条件的整点不只一个,而本题只找出了满足条件的一个解.
解:设每根截500 mm的x根、600 mm的y根,
则 且x、y∈Z.
且x、y∈Z.
可行域如下图所示.

目标函数为z=x+y,
作一组平行直线x+y=t,
经过可行域中的点且和原点距离最远的直线为过点B(8,0)的直线,
这时x+y=8.
由x、y为正整数知(8,0)并不是最优解,
因它不在可行域内.
因此在可行域内找整点,
得到点(2,5),(3,4),(4,3),(5,2),(6,1)均为最优解,
此时x+y=7.
答:每根钢管截500 mm的2根、600 mm的5根或截500 mm的3根、600 mm的4根或截500 mm的4根、600 mm的3根或截500 mm的5根、600 mm的2根或截500 mm的6根、600 mm的1根合理.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com