
【题目】已知c>0,且c≠1,设p:函数y=cx在R上单调递减;q:函数f(x)=x2﹣2cx+1在( ![]() ,+∞)上为增函数,若“p且q”为假,“p或q”为真,求实数c的取值范围.
,+∞)上为增函数,若“p且q”为假,“p或q”为真,求实数c的取值范围.
【答案】解∵函数y=cx在R上单调递减,∴0<c<1.
即p:0<c<1,
∵c>0且c≠1,∴¬p:c>1.
又∵f(x)=x2﹣2cx+1在( ![]() ,+∞)上为增函数,∴c≤
,+∞)上为增函数,∴c≤ ![]() .
.
即q:0<c≤ ![]() ,
,
∵c>0且c≠1,∴¬q:c> ![]() 且c≠1.
且c≠1.
又∵“p或q”为真,“p且q”为假,
∴p真q假,或p假q真.
①当p真,q假时,{c|0<c<1}∩{c|c> ![]() ,且c≠1}={c|
,且c≠1}={c| ![]() }.
}.
②当p假,q真时,{c|c>1}∩{c|0<c ![]() }=.
}=.
综上所述,实数c的取值范围是{c| ![]() }
}
【解析】由函数y=cx在R上单调递减,知p:0<c<1,¬p:c>1;由f(x)=x2﹣2cx+1在( ![]() ,+∞)上为增函数,知q:0<c≤
,+∞)上为增函数,知q:0<c≤ ![]() ,¬q:c>
,¬q:c> ![]() 且c≠1.由“p或q”为真,“p且q”为假,知p真q假,或p假q真,由此能求出实数c的取值范围.
且c≠1.由“p或q”为真,“p且q”为假,知p真q假,或p假q真,由此能求出实数c的取值范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() .
.
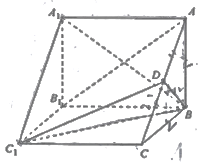
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足Sn=2n﹣an(n∈N*).
(1)计算a1 , a2 , a3 , a4 , 并由此猜想通项公式an;
(2)用数学归纳法证明(Ⅰ)中的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x>0).
(x>0).
(1)试判断函数f(x)在(0,+∞)上单调性并证明你的结论;
(2)若f(x)> ![]() 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(3)求证:(1+1×2)(1+2×3)…[1+n(n+1)]>e2n﹣3 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”近年来成为了百姓耳熟能详的热门词汇,对于旅游业来说,“一带一路”战略的提出,让“丝路之旅”超越了旅游产品、旅游线路的简单范畴,赋予了旅游促进跨区域融合的新理念. 而其带来的设施互通、经济合作、人员往来、文化交融更是将为相关区域旅游发展带来巨大的发展机遇.为此,旅游企业们积极拓展相关线路;各地旅游主管部门也在大力打造丝路特色旅游品牌和服务.某市旅游局为了解游客的情况,以便制定相应的策略. 在某月中随机抽取甲、乙两个景点10天的游客数,统计得到茎叶图如下:

(1)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据,以每天游客人数频率作为概率.今从这段时期内任取4天,记其中游客数超过130人的天数为![]() ,求概率
,求概率![]() ;
;
(2)现从上图20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于125且不高于135人的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
(Ⅰ)求证:EF∥平面PBC;
(Ⅱ)求二面角E﹣DF﹣A的余弦值;
(Ⅲ)在棱PC上是否存在一点G,使GF⊥平面EDF?若存在,指出点G的位置;若不存在,说明理由.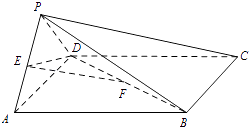
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a3=6,a5+a7=24,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= ![]() (n∈N+),求数列{bn}的前n项和Tn .
(n∈N+),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于数列有下列命题:
①数列{an}的前n项和为Sn , 且Sn=an﹣1(a∈R),则{an}为等差或等比数列;
②数列{an}为等差数列,且公差不为零,则数列{an}中不会有am=an(m≠n),
③一个等差数列{an}中,若存在ak+1>ak>0(k∈N*),则对于任意自然数n>k,都有an>0;
④一个等比数列{an}中,若存在自然数k,使akak+1<0,则对于任意n∈N* , 都有anan+1<0,
其中正确命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com